cho hình bình hành ABCD trên tia đối của tia BA lấy điểm E sao cho B là trung điểm của AE
a,Chứng minh BECD là hình bình hành
b,Gọi O là gia điểm của 2 đường chéo AC và BD
c, Gọi I là trung điểm của CE.Chứng minh tứ giác OBIC là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Xét tứ giác MBCN có
MB//CN
MB=CN
Do đó: MBCN là hình bình hành
b: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
a) Ta có:
M là trung điểm AB
N là trung điểm CD
=> MN là đường trung bình hình bình hành ABCD
=> MN//AD//BC
Xét tứ giác AMND có:
MN//AD
AM//DN
=> AMND là hình bình hành
Xét tứ giác MBCN có:
MN//BC
MB//NC
=> MBCN là hình bình hành
b) Xét tứ giác AMCN có:
\(AM=\dfrac{1}{2}AB\)(M là trung điểm AB)
\(CN=\dfrac{1}{2}CD\)(N là trung điểm CD)
Mà AB=CD(ABCD là hình bình hành)
\(\Rightarrow AM=CN\)
Mà AM//CN(AB//CD,\(M\in AB,N\in CD\))
=> AMCN là hình bình hành

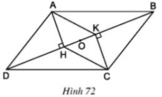
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.

A B C D P Q E F
a) Có \(DE=\frac{1}{2}DA\), \(BF=\frac{1}{2}BC\).
Tứ giác ABCD là hình bình hành nên DE = BC suy ra DE = BF.
Mà DE // BF.
Vì vậy tứ giác BEDF là hình bình hành.
b) Theo chứng minh câu a tứ giác BEDF là hình bình hành suy ra BE // DF.
Xét tam giác ADQ có E là trung điểm của DA và AB // DQ nên P là trung điểm của AQ.
Vì vậy AP = PQ. (1)
Xét tam giác BCP có F là trung điểm của BC và FD // BE nên Q là trung điểm của của PC.
Vì vậy PQ = QC. (2)
Từ (1) và (2) suy ra: AP = PQ = QC.
c)Do AE // BC nên áp dụng định lý Ta-lét:
\(\frac{AP}{PB}=\frac{EP}{PB}=\frac{1}{2}\).
Suy ra \(EP=\frac{1}{2}PB\).
Mặt khác R là trung điểm của PB nên PR = RB \(=\frac{1}{2}PB\).
Từ đó suy ra \(EP=PR=RB\).
Vậy P là trung điểm của AR và ta cũng có P là trung điểm AQ nên tứ giác ARQE là hình bình hành.
Bài này mình làm xong rồi nhưng lỡ tay bấm nút hủy.
MONG CÁC BẠN

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
a: Ta có: BA//CD
mà B\(\in AE\)
nên BE//CD
Ta có: BA=CD
BA=BE
Do đó: BE=CD
Xét tứ giác BECD có
BE//CD
BE=CD
Do đó: BECD là hình bình hành
c: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Ta có: BDCE là hình bình hành
=>BD//CE và BD=CE
Ta có:BD=CE
mà BD=2OB và CE=2CI
nên OB=CI
Xét tứ giác BOCI có
BO//CI
BO=CI
Do đó: BOCI là hình bình hành
có tick,giúp ạ