Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi E, F lần lượt là trung điểm của SA và SB.
a)Chứng minh EF//CD
b)tìm giao điểm M của SC và (ADF)
c)Gọi I là giao điểm của AF và DM. Chứng minh SI//AB//CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2021
a.
Do M là trung điểm SC, N là trung điểm SA \(\Rightarrow MN\) là đường trung bình tam giác SAC
\(\Rightarrow MN||AC\)
Mà \(AC\in\left(ABCD\right)\Rightarrow MN||\left(ABCD\right)\)
Gọi O là giao điểm AC và BD \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
Trong mp (ABCD), kéo dài AB và CD cắt nhau tại E
Trong mp (SCD), nối EM cắt SD tại F
\(\Rightarrow F=SD\cap\left(MAB\right)\)
VM
Vũ Minh Hoàng
CTVHS
VIP
11 tháng 8
Bạn @than thien nếu bạn copy từ AI hay ChatGPT thì hãy xem kỹ các ký tự của bài mình, và khuyên bạn là nên hạn chế sopy AI hay ChatGPT thôi !
6 tháng 1 2024
a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD
6 tháng 1 2024
M,N lần lượt là trung điểm của SB và SB là sai đề rồi bạn. Bạn coi lại đề nha
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
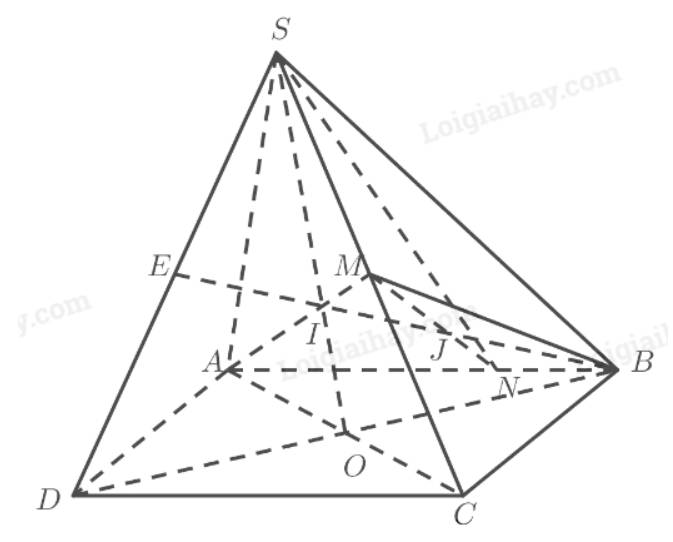
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(AM\) và \(SO\). Ta có:
\(\left. \begin{array}{l}I \in SO \subset \left( {SB{\rm{D}}} \right)\\I \in AM\end{array} \right\} \Rightarrow I = AM \cap \left( {SB{\rm{D}}} \right)\)
Xét tam giác \(SAC\) có:
\(ABCD\) là hình bình hành \( \Rightarrow O\) là trung điểm của \(AC\)
Theo đề bài ta có \(M\) là trung điểm của \(SC\)
Mà \(I = SO \cap AM\)
\( \Rightarrow I\) là trọng tâm của .
b) Gọi \(E\) là giao điểm của \(S{\rm{D}}\) và \(BI\). Ta có:
\(\left. \begin{array}{l}E \in BI \subset \left( {ABM} \right)\\E \in S{\rm{D}}\end{array} \right\} \Rightarrow E = S{\rm{D}} \cap \left( {ABM} \right)\)
c) Gọi \(J\) là giao điểm của \(MN\) và \(BE\). Ta có:
\(\left. \begin{array}{l}J \in BE \subset \left( {SB{\rm{D}}} \right)\\J \in MN\end{array} \right\} \Rightarrow J = MN \cap \left( {SB{\rm{D}}} \right)\)
22 tháng 9 2023
Tham khảo:
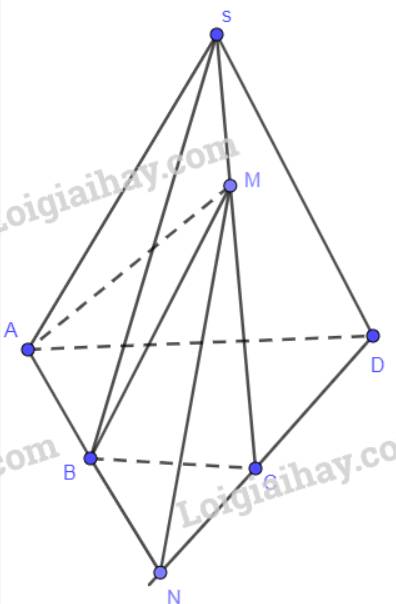
Ta có N thuộc đường thẳng AB , mà AB nằm trong mặt phẳng (ABM) nên N cũng nằm trong mp(ABM)
M và N đều nằm trong mặt phẳng (ABM) nên MN nằm trong mp(ABM) (1)
M thuộc SC suy ra M nằm trong mp(SCD), N thuộc đường thẳng CD nên N nằm trong mp(SCD)
Do đó, MN nằm trong mp(SCD) (2)
Từ (1) và (2) suy ra MN là giao tuyến của hai mp(ABM) và (SCD)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
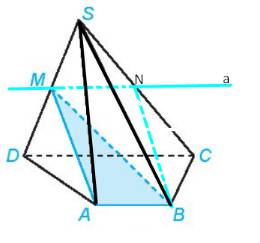
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD
Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB.
b, Do MN //CD và M là trung điểm của SD.
Suy ra, MN là đường trung bình của tam giác SCD.