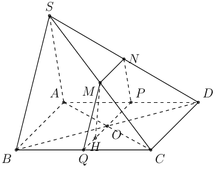
Cho hình chóp S.ABCD có đáy là hình bình hành. M,N,P,Q nằm trên BC,SC,SD,AD sao cho MN//SB, NP//CD, MQ//CD
a)chứng minh PQ//SA
b)K lã giao điểm của MN và PQ. Chứng minh SK//AD//BC
(Giúp vs ạ, cảm ơn nhiều)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 11 2023
a: Gọi O là giao điểm của AC và BD
Chọn mp(SAC) có chứa AN
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi I là giao điểm của SO với AN
=>I là giao điểm của AN với mp(SBD)
Chọn mp(AMN) có chứa MN
\(B\in AM\subset\left(AMN\right)\)
\(B\in BD\subset\left(SBD\right)\)
Do đó: \(B\in\left(AMN\right)\cap\left(SBD\right)\)
mà \(I\in\left(AMN\right)\cap\left(SBD\right)\)
nên (AMN) giao (SBD)=BI
Gọi K là giao điểm của BI với MN
=>K là giao điểm của MN với mp(SBD)
b: K là giao điểm của BI với MN
=>B,I,K thẳng hàng
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC và O là trung điểm của BD
Xét ΔSAC có
O,N lần lượt là trung điểm của CA,CS
=>ON là đường trung bình
=>ON//SA và ON=SA/2
Xét ΔINO và ΔIAS có
\(\widehat{INO}=\widehat{IAS}\)
\(\widehat{NIO}=\widehat{AIS}\)
Do đó: ΔINO đồng dạng với ΔIAS
=>\(\dfrac{IN}{IA}=\dfrac{NO}{AS}=\dfrac{1}{2}\)
20 tháng 12 2021
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
CM
27 tháng 8 2019
Đáp án D
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .
1 tháng 11 2023
a: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA
SA//OM
\(OM\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
b: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA
1 tháng 11 2023
a: XétΔSDB có
M,O lần lượt là trung điểm của DS,DB
=>MO là đường trung bình của ΔSDB
=>MO//SB
SB//MO
MO\(\subset\)(MAC)
SB không nằm trong mp(MAC)
Do đó: SB//(MAC)
b: Xét (OMA) và (SAB) có
\(A\in\left(OMA\right)\cap\left(SAB\right)\)
OM//SB
Do đó: (OMA) giao (SAB)=xy,xy đi qua A và xy//OM//SB
8 tháng 12 2023
Trong mp(SDA), gọi E là giao điểm của SG với AD
Trong mp(SBC), gọi K là giao điểm của SH với BC
Xét ΔSAD có
G là trọng tâm của ΔSAD
E là giao điểm của SG với AD
Do đó: E là trung điểm của AD
Xét ΔSBC có
H là trọng tâm của ΔSBC
SH cắt BC tại K
Do đó: K là trung điểm của BC
Xét hình thang ABCD(AB//CD) có
E,K lần lượt là trung điểm của AD,BC
=>EK là đường trung bình
=>EK//AB
Xét ΔSDE có
SE là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{SG}{SE}=\dfrac{2}{3}\)
Xét ΔSBC có
H là trọng tâm của ΔSBC
SK là đường trung tuyến
Do đó: \(\dfrac{SH}{SK}=\dfrac{2}{3}\)
Xét ΔSEK có \(\dfrac{SG}{SE}=\dfrac{SH}{SK}\left(=\dfrac{2}{3}\right)\)
nên GH//EK
mà EK//AB
nên GH//AB
Ta có: GH//AB
AB\(\subset\)(SAB)
GH không nằm trong mp(SAB)
Do đó: GH//(SAB)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
+) Xét tam giác SAC có SA = SC \( \Rightarrow \) SAC là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) AC.
Xét tam giác SBD có SB = SD \( \Rightarrow \) SBD là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) BD.
+) Ta có SO \( \bot \) AC; SO \( \bot \) BD; AC \( \cap \) BD tại O \( \Rightarrow \) SO \( \bot \) (ABCD).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.