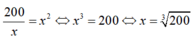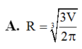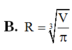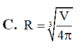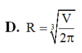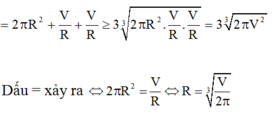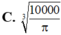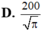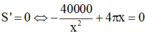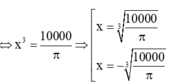một người thợ định làm 1 thùng để đựng 2m^3 nước dạng hình trụ (không nắp) để tiết kiệm vật liệu nhất cần làm đáy của thùng có bán kính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Gọi R, h lần lượt là bán kính đáy và chiều cao của thùng phi.
Thể tích của thùng phi là V = 2 π ⇒ π R 2 h = 2 π ⇒ h = 2 R 2 .
Diện tích toàn phần của thùng phi là S t p = S x q + 2 x S d = 2 π R h + 2 π R 2
Ta có R h + R 2 = R . 2 R 2 + R 2 = R 2 + 1 R + 1 R ≥ 3 R 2 . 1 R . 1 R 3 = 3 ⇒ S t p ≥ 6 π m 2 .
Dấu = xảy ra khi và chỉ khi R 2 = 1 R ⇔ R = 1 → h = 2.

Đáp án C
Đổi 20 lít = 20 000 cm3
Gọi bán kính nắp đậy của thùng sơn là x (cm), x > 0, chiều cao của thùng sơn là h (cm)
Khi đó thể tích của thùng sơn là
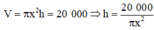
Diện tích toàn phần của thùng sơn là:
![]()
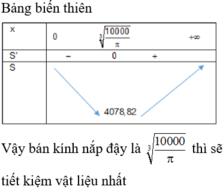
Để nhà sản xuất tiết kiệm được vật liệu nhất tức là Stp nhỏ nhất
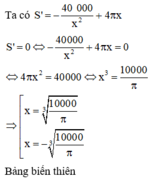
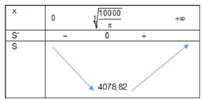
Vậy bán kính nắp đậy là 1000 π 3 thì sẽ tiết kiệm vật liệu nhất

Đáp án là A
Gọi cạnh đáy, cạnh bên của hình hộp đứng lần lượt là x và y ( x ,y > 0)
Ta có:
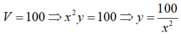
Khi đó:
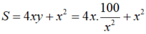
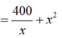
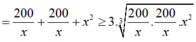
![]()
Vậy S đạt giá trị nhỏ nhất bằng 30 40 3 khi