Khai triển đa thức:
(-x+1)^3Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(2x+1\right)\left(x+3\right)+\left(x+1\right)^2\left(x+2\right)+\left(x+5\right)\left(x+1\right)\)
\(=2x^2+6x+x+3+x^3+2x^2+x+2x^2+4x+2+x^2+x+5x+5\)
\(=x^3+7x^2+18x+10\)
đúng ko nhỉ?
tham khảo : KHAI TRIỂN RÚT GỌN ĐA THỨC BẰNG CASIO (1LINK DUY NHẤT) - YouTube

Lời giải.
Cách 1:
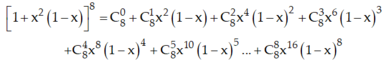
Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8.
Do đó x8 chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là:![]() .
.
Vậy hệ số cuả x8 trong khai triển đa thức 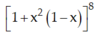 là:
là:
![]()
Cách 2: Ta có:
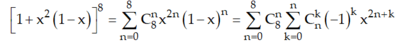
với 0 ≤ k ≤ n ≤ 8.
Số hạng chứa x8 ứng với 2n + k = 8 ⇒ k = 8 -2n là một số chẵn.
Thử trực tiếp ta được k = 0, n =4 và k = 2, n = 3.
Vậy hệ số của x8 là ![]()
Chọn C.

\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....

Lời giải:
\(P(x)=2x(1-x)^{15}=2x\sum \limits_{k=0}^{15}C^k_{15}(-x)^k=2\sum \limits_{k=0}^{15}C^k_{15}(-1)^kx^{k+1}\)
Số hạng chứa $x^{12}$
$\Rightarrow k+1=12\Rightarrow k=11$
Vậy số hạng chứa $x^{12}$ là:
$2C^{11}_{15}(-1)^{11}x^{12}=-2730$

Ta thấy rằng : P ( x ) là một đa thức bậc 3 và có hệ số cao nhất bằng 3 . Do đó ta viết P ( x ) dưới dạng chính tắc như sau :
\(P\left(x\right)=3x^3+Bx^2+Cx+D\)
\(\Rightarrow\left(x-1\right)\left(x-3\right)\left(3x+4\right)+5x-2=3x^3+Bx^2+Cx+D\)
+) Với x =0 ta có D = 10
+) Với x = 1 ta có : 3 = 3 + B + C + 10
=> B + C = -10 ( 1 )
+) Với x = -1 ta có : 1 = -3 + B - C = 10
=> B -C = 6 ( 2 )
Từ (1) và (2) suy ra B = -8 ; C= -2
Vậy \(P\left(x\right)=3x^3-8x^2-2x+10\)

\(A=\left(2x\right)^4+4.\left(2x\right)^3.1+6\left(2x\right)^2.1+4.\left(2x\right).1+1+3^5+5.3^4.x+10.3^3.x^2+10.3^2.x^3+5.3.x^4+x^5\)
\(A=16x^4+32x^3+24x^2+8x+1+243+405x+270x^2+90x^3+15x^4+x^5\)
\(A=x^5+31x^4+122x^3+294x^2+413x+244\)
`(-x+1)^3`
`= (1-x)^3`
`= 1^3 + 3 . 1^2 . (-x) + 3 . 1 . (-x)^2 + (-x)^3`
`= 1 - 3x + 3x^2 - x^3`