Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


kiến thức lớp 8 chưa hok nên ko hỉu!!
5654646457568


Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi

SO EASY!
A B C D E F G H
+) Xét tam giác ABD có :
E là trung điểm của AB
H là trung điểm của AD
=> HE là đường trung bình của tam giác ABD
\(\Rightarrow\hept{\begin{cases}HE//BD\left(1\right)\\HE=\frac{1}{2}BD\left(2\right)\end{cases}}\)
+) Xét tam giác CBD có :
F là trung điểm của BC
G là trung điểm của CD
=> FG là đường trung bình của tam giác CBD
\(\Rightarrow\hept{\begin{cases}FG//BD\left(3\right)\\FG=\frac{1}{2}BD\left(4\right)\end{cases}}\)
Từ ( 1 ) và ( 3 ) \(\Rightarrow HE//FG\)
Từ ( 3 ) và ( 4 ) \(\Rightarrow HE=FG\)
+) Xét tứ giác EFGH có :
HE // FG ; HE = FG
=> EFGH là hình bình hành.
+) Xét tam giác ABC có
E là trung điểm của AB
F là trung điểm của BC
=> EF là đường trung bình của tam giác ABC
=> EF // AC
+) Ta có : HE // BD
Mà \(BD\perp AC\)
\(\Rightarrow HE\perp AC\)
Ta lại có: EF // AC
\(\Rightarrow EF\perp HE\)
\(\Rightarrow\widehat{HEF}=90^o\)
+) Hình bình hành EFGH có góc HEF = 90o
=> EFGH là hình chữ nhật.
Ok đã xong!

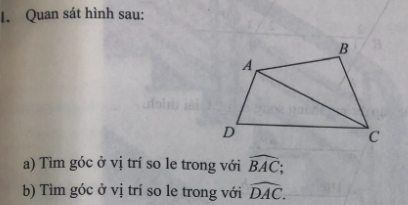
 Giúp mình vs
Giúp mình vs
a: Góc so le trong với \(\widehat{BAC}\) là góc ACD
b: Góc so le trong với \(\widehat{DAC}\) là góc BCA