mọi người giải mã đề giups e với ạ, được mấy bài hay nhiêu đáy ạ, cảm ơn...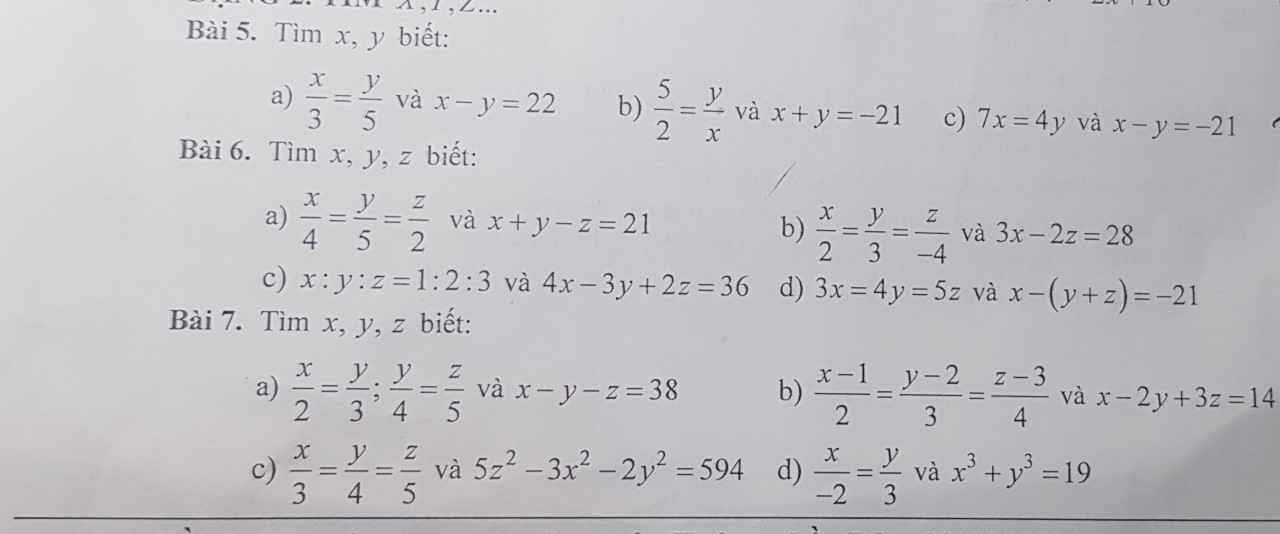
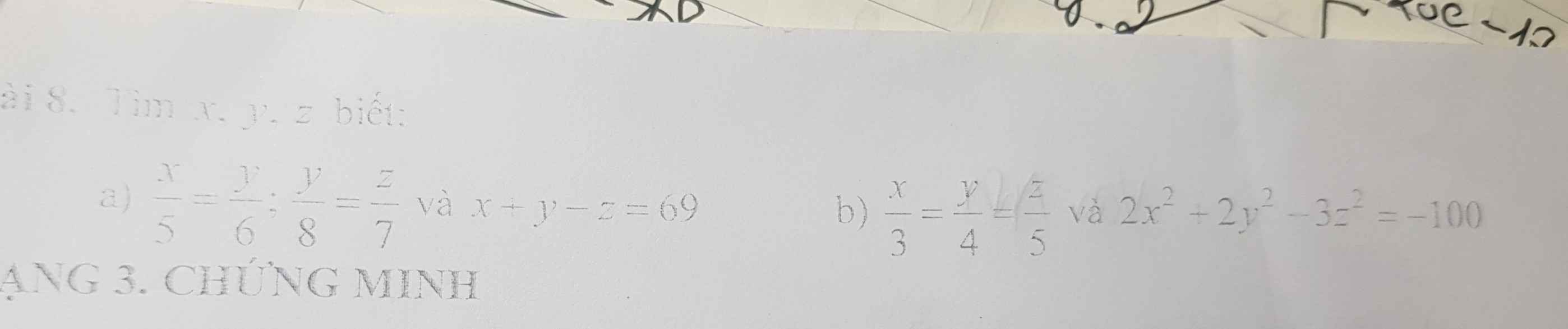
Đọc tiếp
mọi người giải mã đề giups e với ạ, được mấy bài hay nhiêu đáy ạ, cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CH
1
Những câu hỏi liên quan
MV
16 tháng 7 2017
a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
BN
16 tháng 7 2017
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên
15 tháng 2 2016
Bàu 68:
-Các t/c đó đc suy ra từ các định lý:
+a,b)định lý:Tổng ba góc của một tam giác bằng 180°
+c)đl:Trong một tam giác cân,hai góc ở đáy = nhau
+d)đl:Nếu một tam giác có hai góc =nhau thì tam giác đó là tam giác cân
DM
30 tháng 12 2021
HÙGHJUJNHJRJIJKJHJUIRGJUIJUIGJUIGJUIFKJIOJUITJUIKIOUJRJUIGJUTRGJUI6JUHJUIHJYUIJUIGJUIJUIRIGIJUIERGJU6JIGJUIJUITGHJUTJUIHITGJUIYIJH
NT
1
27 tháng 11 2015
bài 22
Xét ΔDAE và ΔBOC có:
AD = OB (gt)
DE = BC (gt)
AE = OC (gt)
Nên ∆DAE= ∆BOC (c.c.c)
suy ra ∠DAE = ∠BOC(hai góc tương tứng)
vậy ∠DAE = ∠xOy.
bài 23
∆BAC và ∆BAD có: AC= AD (gt)
BC = BD(gt)
AB cạnh chung.
Nên ∆BAC= ∆BAD(c.c.c)
Suy ra ∠BAC = ∠BAD (góc tương ứng)
Vậy AB là tia phân giác của góc CAD.
nhớ tick nha!!
LL
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
1
HN
21 tháng 6 2017
Bài 6:
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
29 tháng 11 2016
4.4
TH1: Nếu x<1 thì ta có:
1 - x + 4 - x =3x
5-2x=3x
5=5x
=> x=1 ( k thỏa mãn)
TH2: 1<x<4 thì ta có :
x-1=4x=3x
3=3x
=> x=1 ( thỏa mãn)
TH3:Nếu x >4 thì ta có:
x-1+x-4=3x
2x-5=3x
2x-3x=5
-x=5
=> x=-5 ( k thỏa mãn)
Vậy x=1
BD
2
14 tháng 6 2016
Sử dụng tính chất : nếu a , b , c \(\in\) Z và a < b thì a + c < b - c . Từ đó
=> \(\frac{a}{m}< \frac{a+b}{2m}\) ( chia 2 vế cho m > 0 )
Vậy x < z ( 1 )
- Ta chứng minh z < y hay \(\frac{a+b}{2m}< \frac{b}{m}\)
Ta có : am < bm => am + bm < bm + bm ( cộng hai vế với bm )
=> ( a + b )m < 2bm
=> a + b < 2b ( chia 2 vế cho m )
=> \(\frac{a+b}{2m}< \frac{2b}{2m}=\frac{b}{m}\) ( chia 2 vế cho 2m )
Hay z < y ( 2 )
Từ ( 1 ) và ( 2 ) => x < z < y
* Nhận xét : từ kết quả trên ta rút ra kết luận : trên trục số , giữa 2 điểm hữu tỉ khác nhau bất kì bao giờ cũng có ít nhất một điểm hữu tỉ nữa và do đó có vô số điểm hữu tỉ . Ta bảo tập hợp Q là tập trù mật.
Bài 10:
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^2\cdot k=dk^3\end{matrix}\right.\)
a:
\(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\left(\dfrac{dk^3+dk^2+dk}{dk^2+dk+d}\right)^3=\left(\dfrac{dk\left(k^2+k+1\right)}{d\left(k^2+k+1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{a+b+c}{b+c+d}\right)^3\)
b: Sửa đề: Chứng minh \(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{a}{d}\)
\(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{\left(dk^3\right)^3+\left(dk\right)^3+\left(dk^2\right)^3}{\left(dk\right)^3+\left(dk^2\right)^3+d^3}\)
\(=\dfrac{d^3k^9+d^3k^3+d^3k^6}{d^3k^3+d^3k^6+d^3}=\dfrac{d^3\cdot k^3\left(k^6+1+k^3\right)}{d^3\cdot\left(k^3+k^6+1\right)}=k^3\)
\(=\dfrac{dk^3}{d}=\dfrac{a}{d}\)
Bài 14:
x+y+z=0
=>x+y=-z; x+z=-y; y+z=-x
\(A=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\cdot\left(-x\right)\cdot\left(-y\right)\)
=-xyz
=-2