Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 4 :
24 phút = \(\dfrac{24}{60} = \dfrac{2}{5}\) giờ
Gọi thời gian dự định đi từ A đến B là x(giờ) ; x > 0
Suy ra quãng đường AB là 36x(km)
Khi vận tốc sau khi giảm là 36 -6 = 30(km/h)
Vì giảm vận tốc nên thời gian đi hết AB là x + \(\dfrac{2}{5}\)(giờ)
Ta có phương trình:
\(36x = 30(x + \dfrac{2}{5})\\ \Leftrightarrow x = 2\)
Vậy quãng đường AB dài 36.2 = 72(km)

Giải
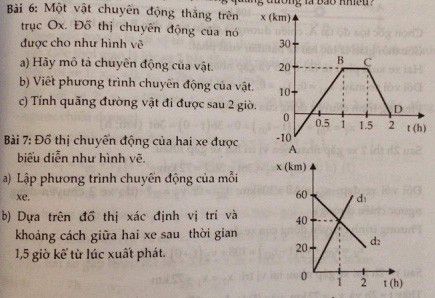
a. Phương trình chuyển động của hai xe
Xe ô tô: x1=30t
Xe mô tô: x2= 100 - 20t
b. Đồ thị toạ độ- thời gian, xác định
vị trí và thời điểm hai xe gặp nhau.
+ Chọn hệ toạ độ như hình vẽ:
+ Đồ thị toạ độ:
Của ô tô: Đoạn thẳng OM
Của mô tô: Đoạn thẳng PM
+ Vị trí hai xe gặp nhau: Cách gốc tạo độ 60km, thời
điểm hai xe gặp nhau là lúc 2h

Bài 2:
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=-x+3\)
\(\Leftrightarrow2x^2+x-3=0\)
\(\Leftrightarrow2x^2-2x+3x-3=0\)
\(\Leftrightarrow2x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot1^2=2\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Vậy: Tọa độ giao điểm của (p) và (D) là (1;2) và \(\left(-\dfrac{3}{2};\dfrac{9}{2}\right)\)




 (1)
(1)

a: 15:(x+2)=3
=>\(x+2=\dfrac{15}{3}=5\)
=>x=5-2=3
b: 20(1+x)=2
=>\(x+1=\dfrac{2}{20}=\dfrac{1}{10}\)
=>\(x=\dfrac{1}{10}-1=-\dfrac{9}{10}\)
f: \(12x-33=3^2\cdot3^3\)
=>\(12x-33=3^5=243\)
=>12x=243+33=276
=>\(x=\dfrac{276}{12}=23\)
g: 541+(218-x)=73
=>218-x=73-541=-468
=>x=218+468=686