Cho tam giác ABC vuông tại A có BC = 2 cm và tanB = √3. Tính AB, AC?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2021
Gọi mỗi góccòn lại trên giấy ô vuông là K; M; N
Xét Tg AMB vuông tại M ta có:
AB^2 = AM^2 + MB^2 (định lí Pi-ta-go)
Thay số: AB^2 = 22 + 12 = 5
=> AB = căn 5
Xét Tg ANC vuông tại N ta có:
AC^2 = AN^2 + NC^2 (định lí Pi-ta-go )
AC^2= 32 + 42 = 25
=> AC = 5
Xét Tg BKC vuông tại K ta có:
BC^2= BK^2+ KC^2(định lí Pi-ta-go )
BC^2 = 32 + 52 = 34
=>BC= căn 34
1 tháng 1 2018
A B C 16,6 CM 12,7CM
diện tích tam giác ABC là
\(\left(12,7\times15,6\right)\div2=99,06\left(cm^2\right)\)
đáp số : \(99,06cm^2\)
2 tháng 1 2019
Diện tích hình tam giác vuông abc là :
15.6 x 12.7 : 2 = 99.06 ( cm2 )
Đáp số : 99.08 cm2
22 tháng 1 2022
Bài 3:
Gọi độ dài hai cạnh góc vuông lần lượt là a,b
Theo đề, ta có: a/8=b/15
Đặt a/8=b/15=k
=>a=8k; b=15k
Ta có: \(a^2+b^2=51^2\)
\(\Leftrightarrow289k^2=2601\)
=>k=3
=>a=24; b=45
Bài 6:
Xét ΔABC có \(10^2=8^2+6^2\)
nên ΔABC vuông tại A
22 tháng 1 2022
Refer:
2,
Ta có:AH là đường cao ΔABC
⇒AH ⊥ BC tại H
⇒∠AHB=∠AHC=90°
⇒ΔAHB và ΔAHC là Δvuông H
Xét ΔAHB vuông H có:
AH² + HB²=AB²(Py)
⇔24² + HB²=25²
⇔ HB²=25² - 24²
⇔ HB²=49
⇒ HB=7(đvđd)
Chứng minh tương tự:HC=10(đvđd)
Ta có:BC=BH + CH=7 + 10=17(đvđd)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 5 2022
Độ dài cạnh AB so với cạnh BC là: \(\dfrac{3}{4}\)x \(\dfrac{4}{5}\) =\(\dfrac{3}{5}\)
Độ dài cạnh AB là: 72:(3+4+5)x3= 18(cm)
Độ dài cạnh AC là: 72:(3+4+5)x4 = 24(cm)
Diện tích tam giác ABC là: 18x24:2 = 216(\(cm^2\))
Đáp số: 216cm2
CM
19 tháng 2 2018
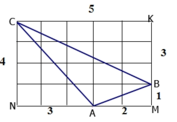
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34
AH
Akai Haruma
Giáo viên
5 tháng 2 2024
Lời giải:
Coi độ dài cạnh AB là 3 phần thì độ dài cạnh AC là 4 phần, độ dài cạnh BC là 5 phần.
Tổng số phần bằng nhau: $3+4+5=12$ (phần)
Độ dài cạnh AB: $144:12\times 3=36$ (cm)
Độ dài cạnh AC: $144:12\times 4=48$ (cm)
Diện tích tam giác $ABC$: $36\times 48:2=864$ (cm2)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{AB}=\sqrt{3}\)
=>\(\dfrac{AC^2}{AB^2}=3\)
=>\(AC^3=3AB^2\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(4\cdot AB^2=2^2=4\)
=>\(AB^2=1\)
=>AB=1(cm)
=>\(AC=1\cdot\sqrt{3}=\sqrt{3}\left(cm\right)\)