Cho tam giác ABC. Hãy xác định trên cạnh BC một điểm E và trên cạnh AB một điểm D sao cho BD = DE = EC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


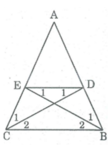
Ta có: BD = DE ⇒ ∆ BDE cân tại D
∠ B 1 = ∠ E 1
Mà ∠ E 1 = ∠ B 2 (so le trong)
⇒ ∠ B 1 = ∠ B 2
DE = EC ⇒ ∆ DEC cân tại E
⇒ ∠ D 1 = ∠ C 1
∠ D 1 = ∠ C 2 (so le trong)
⇒ ∠ C 1 = ∠ C 2
Vậy khi BE là tia phân giác của ∠ (ABC) , CD là tia phân giác của ∠ (ACB) thì BD = DE = EC

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc CB
c: BA=BE
DA=DE
=>BD là trung trực của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
Muốn vẽ dc hình, trc hết xác định tam giác cần vẽ cân tại \(\widehat{B}\)
Vì \(BD=DE=EC\)nên D là trung điểm AB và E là trung điểm BC(hay DE là đường trung bình của tam giác)
Vẽ trên mày khó chính xác, bn thông cảm !