cho tam giác abc vuông tại a gọi i là giao điểm của các đường phân giác biết b = √5 ic = căn 10 tính bc và ac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


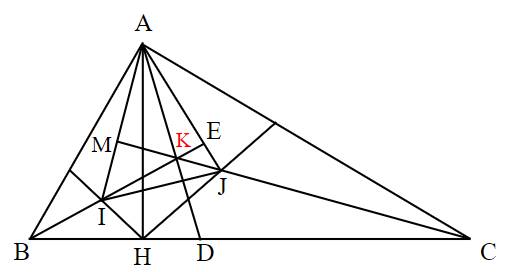
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)

A B C D H I J E K M
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900
. Mà ^EBA=^EAC => ^EBA+^BAE=900
.
Xét tam giác ABE: ^EBA+^BAE=900
=> ^AEB=900
.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900
=> ^ACM+^MAC=900
=> Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)