Cho 3 số a, b, c thoả mãn điều kiện abc= 2023. Tính giá trị biểu thức
P= 2023a^\(^{ }\)2bc/ab+2023a+2023. + ab^2c/bc+b+2023. + abc^2/ac+c+1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
29 tháng 3 2023
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{x}=\dfrac{x+y+z}{y+z+x}=\dfrac{x+y+z}{x+y+z}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\)
Do đó \(\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\)
Thay vào biểu thức \(P=\left(x-y\right)^{2022}+\left(y-z\right)^{2023}+\left(x-z-1\right)^{202}\),ta có:
\(P=0^{2022}+0^{2023}+\left(-1\right)^{202}\)
\(=0+0+1\)
\(=1\)
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
Lời giải:
Áp dụng BĐT AM-GM:
\(x\sqrt{2020-y^2}+y\sqrt{2020-z^2}+z\sqrt{2020-x^2}\leq \frac{x^2+(2020-y^2)}{2}+\frac{y^2+(2020-z^2)}{2}+\frac{z^2+(2020-x^2)}{2}=3030\)Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} x^2=2020-y^2\\ y^2=2020-z^2\\ z^2=2020-x^2\end{matrix}\right.\Rightarrow x=y=z=\sqrt{1010}\)
Khi đó:
$A=3(\sqrt{1010})^2=3030$
H9
HT.Phong (9A5)
CTVHS
6 tháng 12 2023
\(5x^2+2y^2+6xy-8x-4y+4=0\)
\(\Leftrightarrow4x^2+x^2+y^2+y^2+2xy+4xy-8x-4y+4=0\)
\(\Leftrightarrow\left(4x^2+y^2+4+4xy-8x-4y\right)+\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow\left[\left(2x\right)^2+4xy+y^2-4\left(2x+y\right)+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left[\left(2x+y\right)^2-2\cdot\left(2x+y\right)\cdot2+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Ta có: \(\left\{{}\begin{matrix}\left(2x+y-2\right)^2\ge0\forall x,y\\\left(x+y\right)^2\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2\ge0\forall x,y\)
Mặt khác: \(\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}2x+y-2=0\\x+y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(-y\right)+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2y+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=2\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=2\end{matrix}\right.\)
Thay x,y vào P ta có:
\(P=2^{2023}+\left(-2\right)^{2023}=2^{2023}-2^{2023}=0\)
Vậy: ...
DM
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 12 2023
olm sẽ hướng dẫn em làm bài này như sau:
Bước 1: em giải phương trình tìm; \(x\); y
Bước 2: thay\(x;y\) vào P
(\(x-1\))2022 + |y + 1| = 0
Vì (\(x-1\))2022 ≥ 0 ∀ \(x\); |y + 1| ≥ 0 ∀ y
⇒ (\(x\) - 1)2022 + |y + 1| = 0
⇔ \(\left\{{}\begin{matrix}\left(x-1\right)^{2022}=0\\y+1=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\) (1)
Thay (1) vào P ta có:
12023.(-1)2022 : )(2.1- 1)2022 + 2023
= 1 + 2023
= 2024
24 tháng 8 2023
\(M=x^{2023}-2023.\left(x^{2022}-x^{2021}+x^{2020}-x^{2019}+...+x^2-x\right)\)
Ta có : \(x=2022\Rightarrow x+1=2023\)
\(\Rightarrow M=x^{2023}-\left(x+1\right).\left(x^{2022}-x^{2021}+x^{2020}-x^{2019}+...+x^2-x\right)\)
\(\Rightarrow M=x^{2023}-\left(x+1\right)x^{2022}+\left(x+1\right)x^{2021}-\left(x+1\right)x^{2020}+\left(x+1\right)x^{2019}+...-\left(x+1\right)x^2+\left(x+1\right)x\)
\(\Rightarrow M=x^{2023}-x^{2023}-x^{2022}+x^{2022}+x^{2021}-x^{2021}-x^{2020}+x^{2020}+x^{2019}-x^{2019}-...-x^3-x^2+x^2+x\)
\(\Rightarrow M=x\)
\(\Rightarrow M=2022\)
Vậy \(M=2022\left(tạix=2022\right)\)
17 tháng 12 2023
a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)
\(\left|x-1\right|^{2023}>=0\forall x\)
=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)
mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)
nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)
=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)
\(P=x^{2023}+\left(y-10\right)^{2023}\)
\(=1^{2023}+\left(9-10\right)^{2023}\)
=1-1
=0
c: \(\left|x-3\right|>=0\forall x\)
=>\(\left|x-3\right|+2>=2\forall x\)
=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)
mà \(\left|y+3\right|>=0\forall y\)
nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)
=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)
Dấu '=' xảy ra khi x-3=0 và y-3=0
=>x=3 và y=3
CM
25 tháng 7 2019
+ Tìm điều kiện xác định:
Biểu thức xác định khi tất cả các phân thức đều xác định.
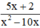xác định ⇔ x2 – 10x ≠ 0
⇔ x(x – 10) ≠ 0
⇔ x ≠ 0 và x – 10 ≠ 0
⇔ x ≠ 0 và x ≠ 10
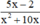xác định ⇔ x2 + 10x ≠ 0
⇔ x(x + 10) ≠ 0
⇔ x ≠ 0 và x + 10 ≠ 0
⇔ x ≠ 0 và x ≠ -10
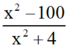luôn xác định vì x2 + 4 > 0 với mọi x ∈ R.
Vậy điều kiện xác định của biểu thức là x ≠ 0 và x ≠ ±10
+ Rút gọn biểu thức:
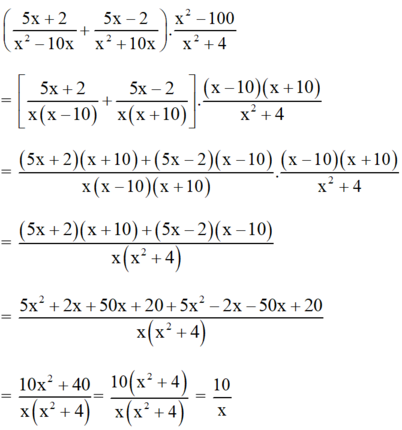
+ Tại x = 20040, giá trị biểu thức bằng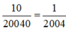 
11 tháng 12 2023
a:
ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b: \(A=\left(\dfrac{x-2}{2x-2}+\dfrac{3}{2x-2}-\dfrac{x+3}{2x+2}\right):\left(1-\dfrac{x-3}{x+1}\right)\)
\(=\left(\dfrac{x-2}{2\left(x-1\right)}+\dfrac{3}{2\left(x-1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right):\dfrac{x+1-x+3}{x+1}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)+3\left(x+1\right)-\left(x+3\right)\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2-x-2+3x+3-x^2-2x+3}{2\left(x-1\right)}\cdot\dfrac{1}{2}\)
\(=\dfrac{-2}{4\left(x-1\right)}=\dfrac{-1}{2\left(x-1\right)}\)
Khi x=2005 thì \(A=\dfrac{-1}{2\cdot\left(2005-1\right)}=-\dfrac{1}{4008}\)
Vì x=1 không thỏa mãn ĐKXĐ
nên khi x=1 thì A không có giá trị
c: Để A=-1002 thì \(\dfrac{-1}{2\left(x-1\right)}=-1002\)
=>\(2\left(x-1\right)=\dfrac{1}{1002}\)
=>\(x-1=\dfrac{1}{2004}\)
=>\(x=\dfrac{1}{2004}+1=\dfrac{2005}{2004}\left(nhận\right)\)