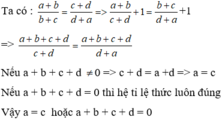Chứng minh rằng nếu 0<a<1 thì căn a > a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
8 tháng 9 2019
Ta có: a b < a + c b + c
⇔ a(b + c) < (a + c)b
(vì a > 0, b > 0 và c > 0 ⇔ b + c > 0 và a + c > 0)
⇔ ab + ac < ab + bc
⇔ ac < bc ⇔ a < b (luôn đúng, theo gt)
ND
0
PT
1
CM
23 tháng 10 2017
Áp dụng kết quả bài 5, ta có: 
⇒ ad < bc (1)
Cộng cả hai vế của (1) với ab ta có: ab + ad < ab + bc
hay a(b + d) < b.(a + c)
Cộng cả hai vế của (1) với cd ta có: ad + cd < bc + cd
Hay d(a + c) < c(b + d)
Vậy 
PT
1
CM
2 tháng 12 2017
Ta có: a b < c d ⇒ a d < b c n ê n
a b + a d < a b + b c ⇔ a ( b + d ) < b ( a + c ) ⇔ a b < a + c b + d
Mặt khác:
a d + c d < b c + d c ⇔ d ( a + c ) < c ( b + d ) ⇔ a + c b + d < c d
Từ (1) và (2): a b < a + c b + d < c d
29 tháng 11 2021
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
NN
1
AH
Akai Haruma
Giáo viên
6 tháng 3 2021
Lời giải:
Khi $x-y+z=0\Rightarrow y=x+z$. Thay vào biểu thức $xy+yz-xz$ thì:
$xy+yz-xz=x(x+z)+(x+z)z-xz=x^2+xz+z^2=x^2+\frac{xz}{2}+\frac{xz}{2}+\frac{z^2}{4}+\frac{3}{4}z^2$
$=(x+\frac{z}{2})^2+\frac{3}{4}z^2$
Dễ thấy $(x+\frac{z}{2})^2\geq 0; \frac{3}{4}z^2\geq 0$ với mọi $x,y,z$ nên $xy+yz-xz\geq 0$
Ta có đpcm.
15 tháng 4 2020
ơi STN = số thứ nhất
STH = SỐ THỨ 2 NHÉ
STB = SỐ THỨ 3 NHA
PT
1
CM
8 tháng 4 2019
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
Mặt khác, với x < 0 thì 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
