Trong hộp có 7 viên bi xanh, 13 viên bi đỏ và 17 viên bi vàng. Hỏi không cần nhìn vào hộp cần bốc ít nhất bao nhiêu viên bi để có chắc chắn 3 viên bi khác màu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2020
Trường hợp xấu nhất xảy ra khi ta lấy 13 viên vàng, 18 viên đỏ và 9 viên xanh. Lúc này chỉ cần lấy thêm một viên nữa thì sẽ đạt yêu cầu.
Vậy cần ít nhất số bi ta lấy là : 13 + 18 + 10 = 41 ( viên bi )
Đ/s : 41 viên bi
21 tháng 8 2020
Trong trường hợp xấu nhất nếu ta lấy hết 18 viên bi đỏ và 13 xanh rồi thì chỉ cần lấy ra 8 viên nữa thì hoàn thành yêu cầu
Cần lấy ra ít nhất số viên bi là
25 + 18 + 8= 51 ( viên )
Đáp số : 51 viên
TT
22 tháng 9 2015
Coi như xui xẻo lấy ra 7 viên toàn bi đỏ thì cần lấy thêm 3 viên nữa như vậy cần ít nhất 10 lần để chăc chắn lấy đc 3 viên bi xanh 2 viên bi đỏ
CM
31 tháng 5 2018
Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:
● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có 
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có 
cách.
Do đó trường hợp này có 
cách.
● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có 
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có 
cách.
Do đó trường hợp này có 
cách.
● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có 
cách.
Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có 
cách.
Do đó trường hợp này có 
cách.
Suy ra số phần tử của biến cố A là 
Vậy xác suất cần tính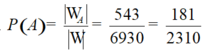 
Chọn B.
5 tháng 12 2015
bài này cần sự thực tiễn
Lấy 5 viên thì lỡ 5 viên bi đều xanh ==> không được
Lấy 6 viên thì lỡ 5 viên bi đều xanh, có 1 đỏ ==> không được
Lấy 7 viên thì lỡ 7 viên bi đều đỏ ==> không được
Lấy 8 viên thì lỡ 7viên bi đều đỏ,1 xanh ==> không được
Lấy 9 viên thì lỡ 7 viên bi đều đỏ, 2 xanh ==> không được
lấy 10 viên, dù có lỡ 7 đỏ cũng còn 3 xanh. OK
18 tháng 9 2015
Để lấy chắc chắn ít nhất 2 viên bi đỏ bạn phải lấy ít nhất 7 viên. ( 5 bi xanh + 2 bi đỏ, đây là trường hợp ít bi đỏ nhất, các trường hợp khác số viên bi đỏ có thể lớn hơn 2).
Để lấy chắc chắn ít nhất 3 viên bi xanh bạn phải lấy ít nhất 10 viên. ( 7 bi đỏ + 3 bi xanh, đây là trường hợp ít bi xanh nhất, các trường hợp khác bi xanh có thể lớn hơn 3).
Vậy để lấy chắc chắn 2 bi đỏ và 3 bi xanh bạn phải lấy ít nhất 10 viên bi (hợp của 2 tập hợp). Khi đó bi xanh chắc chắn ≥ 10, bi đỏ >2.
D
18 tháng 11 2015
tick nha cách làm luôn đó
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
18 tháng 11 2015
Để lấy chắc chắn ít nhất 2 viên bi đỏ bạn phải lấy ít nhất 7 viên. ( 5 bi xanh + 2 bi đỏ, đây là trường hợp ít bi đỏ nhất, các trường hợp khác số viên bi đỏ có thể lớn hơn 2).
Để lấy chắc chắn ít nhất 3 viên bi xanh bạn phải lấy ít nhất 10 viên. ( 7 bi đỏ + 3 bi xanh, đây là trường hợp ít bi xanh nhất, các trường hợp khác bi xanh có thể lớn hơn 3).
Vậy để lấy chắc chắn 2 bi đỏ và 3 bi xanh bạn phải lấy ít nhất 10 viên bi (hợp của 2 tập hợp). Khi đó bi xanh chắc chắn ≥ 10, bi đỏ >2.
16 viên
Trường hợp xấu nhất. Trong 30 lần bốc được 17 bi vàng, và 13 bi đỏ.
Vậy, cần bốc ít nhất 31 viên bi để chắc chắn có 3 viên bi khác màu