
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

Trong tam giác ABC ta có:
E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ED//BC⇒ED//BC và ED=\(\frac{1}{2}BC\) (tính chất đường trung bình của tam giác)
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung bình hình thang BCDE ⇒ MN // DE
\(MN=\frac{DE+BC}{2}=\frac{\frac{BC}{2}+BC}{2}=\frac{3BC}{4}\)(tính chất đường trung bình hình thang)
Trong tam giác BED ta có:
M là trung điểm của BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
\(\Rightarrow MI=\frac{1}{2}DE=\frac{1}{4}BC\)(tính chất đường trung bình tam giác)
Trong tam giác CED ta có:
N là trung điểm của CD
NK // DE
Suy ra: NK là đường trung bình của ∆ BED
\(\Rightarrow NK=\frac{1}{2}DE=\frac{1}{4}BC\)(tính chất đường trung bình tam giác)
\(IK=MN-\left(MI+NK\right)\)
\(=\frac{3}{4}BC-\left(\frac{1}{4}BC+\frac{1}{4}BC\right)=\frac{1}{4}BC\)
\(\Rightarrow MI=IK=KN=\frac{1}{4}BC\)
Chúc bạn học tốt !!!
Cảm ơn hoang viet nhat nhé, nhưng lời giải này không được cô giáo mình chấp nhận vì cô bảo chưa học đến đường trung bình của hình thang nên nếu mình làm thế trên bảng thì các bạn sẽ không hiểu.

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

a: Xét ΔABC có
P là trung điểm của AB
N là trung điểm của AC
Do đó: PN là đường trung bình của ΔABC
Suy ra: PN//CF
Xét tứ giác CPNF có
CP//NF
CF//NP
Do đó: CPNF là hình bình hành

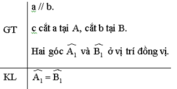
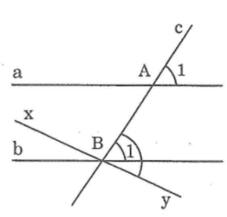
Chứng minh
Giả sử ∠(A1) ≠ ∠(B1)
Qua B kẻ đường thẳng xy sao cho ∠(ABy) = ∠(A1)
Mà hai góc này ở vị trí so le trong nên theo dấu hiệu của hai đường thẳng song song, ta có xy //a
+) Qua điểm B ta kẻ được hai đường thẳng b và xy cùng song song với đường thẳng a. Theo tiên đề Ơ- clit suy ra đường thẳng xy trùng với đường thẳng b.

Gt và câu c viết nhầm phải không bạn? Trung tuyến BD,CE,AM chứ. Còn câu b phải qua B kẻ đường thẳng // FD nhỉ? Nếu thế thì lời giải thế này
(lời giải hơi dài tí)
*Xét tứ giác DEMC:
\(ED=\frac{1}{2}BC\)(cma)
\(CM=\frac{1}{2}BC\)(gt)
\(\Rightarrow ED=CM\)
Mà ED//BC (Cma); \(M\in BC\left(gt\right)\)=> ED//CM
Từ 2 chứng minh trên => DEMC là hbh
=>CD//EM(1)
*Mặt khác, ta có: DF//CE(cmb); DF=CE(cmb)
DF//BP(cmc); DF=BP(cmc)
=> CE//BP(cùng //DF); CE=BP(cùng = DF)
Từ chứng minh trên => CEBP là hbh
Nên 2 đường chéo PE và CB cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm CB (gt) => M cũng là trung điểm PE
hay P,M,E thẳng hàng(2)
Từ (1),(2) CD//EP
=> CDEP là hình thang

a) Ta có:
\(\left\{{}\begin{matrix}AB\perp AC\\KH\perp AC\end{matrix}\right.=>AB//KH\)
b) Ta có:
\(\widehat{ABK}=\widehat{BKI}\left(=60^o\right)\)
Mà hai góc này ở vị trí so le trong
=> AB//KI
c) AB//HK = > \(\widehat{ABK}+\widehat{HKB}=180^o\)
Mà: \(\widehat{ABK}=\widehat{BKI}\)
\(=>\widehat{BKI}+\widehat{HKB}=180^o\)
=> \(\widehat{HKI}\) là góc bẹt hay H, K, I thẳng hàng