
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Độ lớn lực đẩy theo phương ngang: \(F_x=F.cos45^0=80.cos45^0=40\sqrt{2}\left(N\right)\)
Độ lớn lực đẩy theo phương thẳng đứng: \(F_y=F.sin45^0=80.sin45^0=40\sqrt{2}\left(N\right)\)
b. Gia tốc chuyển động: \(a=\dfrac{v}{t}=\dfrac{1,2}{3}=0,4\left(\dfrac{m}{s^2}\right)\)
Áp dụng định luật II Newton có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\) (*)
Chiếu (*) lên phương Ox, chiều dương trùng với chiều chuyển động:
\(F_x-F_{ms}=ma\)
\(\Leftrightarrow40\sqrt{2}-F_{ms}=15.0,4\)
\(\Rightarrow F_{ms}=40\sqrt{2}-6\left(N\right)\)

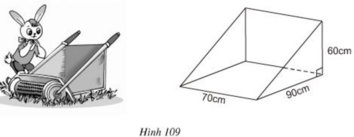
Lăng trụ đứng tam giác có đáy là tam giác vuông, nên diện tích đáy là:
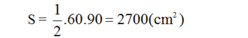
Thể tích lăng trụ V = Sh = 2700.70 = 189000 (cm3)
Vậy dung tích của thùng là 189000cm3

Lăng trụ đứng tam giác có đáy là tam giác vuông, nên diện tích đáy là:
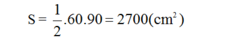
Thể tích lăng trụ V = Sh = 2700.70 = 189000 (cm3)
Vậy dung tích của thùng là 189000cm3

S2quạt =2 n . pi .62/ 360 ; với n =30 độ ( sin n =3/6 =1/2 )
= 6\(\pi\) m2
Stam giác = 1/2 . 3 . \(\sqrt{6^2-3^2}\) = \(\frac{9\sqrt{3}}{2}\)
S cỏ còn lại = S hình tròn - ( S2 quạt + S tam gics ) = .............

máy cắt cỏ ở vườn thứ 2 hết số thời gian là:
5 giờ 15 phút - 2 giờ 45 phút=2 giờ 30 phút
đ/s:2 giờ 30 phút

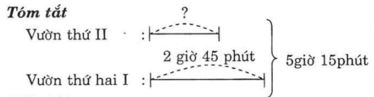
Thời gian máy cắt hết cỏ ở khu vườn thứ hai là :
5 giờ 15 phút – 2 giờ 45 phút = 2 giờ 30 phút
Đáp số : 2 giờ 30 phút.

a: Diện tích sân vườn là 36:4/5=45(m2)
b: Đề hỏi gì vậy bạn?

Máy cắt cỏ ở khu vườn thứ 2 mất số thời gian là:
5 giờ 15 phút - 2 giờ 45 phút = 2 giờ 30 phút
Đáp số: 2 giờ 30 phút
Tk cho mik nhé! Cảm ơn bạn!

Đổi 5h15' = 315'
2h15' = 135'
máy cắt cỏ ở khu vườn thứ hai mất số thời gian là
315 - 135 = 180'
Đổi 180' = 3 h
Đ/S:3h
8. Gọi số vé loại I và loại II lần lượt là x và y
ĐK: x,y > 0
Tổng số vé bán được là 500 vé `=> x+y=500` (1)
Tổng số tiền vé bán được là 44500000 đồng nên ta có pt:
`100000x+75000y=44500000`
`<=>4x+3y=1780` (2)
Từ (1) và (2) ta có hpt: \(\left\{{}\begin{matrix}x+y=500\\4x+3y=1780\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=280\\y=220\end{matrix}\right.\left(tm\right)\)
Vậy: ...