
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
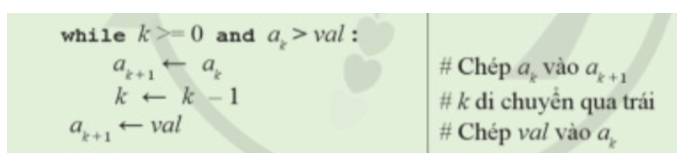
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1


Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

a: \(\left(\dfrac{x+2}{x+1}-\dfrac{2x}{x-1}\right)\cdot\dfrac{3x+3}{x}+\dfrac{4x^2+x+7}{x^2-x}\)
\(=\dfrac{x^2+x-2-2x^2-2x}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{3\left(x+1\right)}{x}+\dfrac{4x^2+x+7}{x\left(x-1\right)}\)
\(=\dfrac{-x^2-x-2}{x-1}\cdot\dfrac{3}{x}+\dfrac{4x^2+x+7}{x\left(x-1\right)}\)
\(=\dfrac{-3x^2-3x-6+4x^2+x+7}{x\left(x-1\right)}=\dfrac{x^2-2x+1}{x\left(x-1\right)}=\dfrac{x-1}{x}\)

Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.
Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.
Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.

a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)

\(=\left(\dfrac{1}{2}+\dfrac{1}{2}\right)-\left(\dfrac{5}{41}+\dfrac{36}{41}\right)=1-1=0\)

Bài 1:
b: \(=\dfrac{x+3-4-x}{x-2}=\dfrac{-1}{x-2}\)
Bài 2:
a: \(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}\)
\(=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)
d: \(=\dfrac{3}{2x^2y}+\dfrac{5}{xy^2}+\dfrac{x}{y^3}\)
\(=\dfrac{3y^2+10xy+2x^3}{2x^2y^3}\)
e: \(=\dfrac{x^2+2xy+x^2-2xy-4xy}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2x^2-4xy}{\left(x+2y\right)\cdot\left(x-2y\right)}=\dfrac{2x}{x+2y}\)

Đánh giá được mức đơn giản của thuật toán, từ đó tìm ra được cách giải nhanh nhất.


\(a)17\cdot85+15\cdot17-120\\ =17\cdot\left(85+15\right)-120\\ =17\cdot100-120\\ =1700-120\\ =1580\\ b)5\cdot7^2-24:2^3\\ =5\cdot49-24:8\\ =245-3\\ =242\\ c)3^3\cdot22-27\cdot19\\ =27\cdot22-27\cdot19\\ =27\cdot\left(22-19\right)\\ =27\cdot3\\ =81\\ d)-\left|-13\right|+\left(-23\right)\\ =-13+\left(-23\right)\\ =-36\\ e)-\left|-13\right|+\left|-25\right|+\left|12\right|\\ =-13+25+12\\ =12+12\\ =24\\ f)23-\left(12-4^2\right)+\left|15\right|\\ =23-\left(12-16\right)+15\\ =23-\left(-4\right)+15\\ =23+4+15\\ =27+15\\ =42\)