 Làm câu 1 , câu 2thôi được ko ah
Làm câu 1 , câu 2thôi được ko ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 6:
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).




a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên

Bạn chụp cho mik trang đấy với, chứ mik lớp 7 rồi còn đâu sách lớp 5 nữa, sách lớp 5 em mik mang đi hok r
a) 8 và 40
8 : 40 = 0,2 = 20%
b) 40 và 8
40 : 8 = 5 = 500%
c) 9,25 và 25
9,25 : 25 = 0,37 = 37%


 giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1

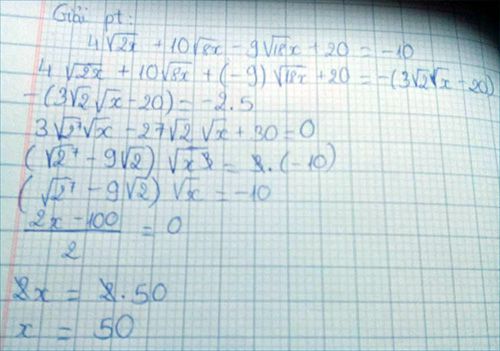



câu g là 1 và 1/7 ạ?
\(1,\)
\(a,\dfrac{-9}{51}.\dfrac{17}{6}\)
\(=-1.\dfrac{1}{2}\)
\(=-\dfrac{1}{2}\)
\(b,\dfrac{-25}{32}.\left(-0,2\right)\)
\(=\dfrac{-25}{32}.-\dfrac{2}{10}\)
\(=\dfrac{-5}{16}.-\dfrac{1}{2}\)
\(=\dfrac{5}{32}\)
\(c,-15,2.3,5=-53,2\)
\(d,\dfrac{-8}{15}.1\dfrac{1}{4}\)
\(=\dfrac{-8}{15}.\dfrac{5}{4}\)
\(=\dfrac{-2}{3}.\dfrac{1}{1}\)
\(=\dfrac{-2}{3}\)
\(e,1\dfrac{2}{5}.\dfrac{-3}{14}\)
\(=\dfrac{7}{5}.\dfrac{-3}{14}\)
\(=\dfrac{1}{5}.\dfrac{-3}{2}\)
\(=-\dfrac{3}{10}\)
\(g,1\dfrac{1}{17}.1\dfrac{1}{36}\)
\(=\dfrac{18}{17}.\dfrac{37}{36}\)
\(=\dfrac{1}{17}.\dfrac{37}{2}\)
\(=\dfrac{37}{34}\)
\(#T.T\)