
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài tham khảo
Cách 1:2 phân số lớn nhất 7/3 và 7/4
Tổng 7/3+7/4=49/12
2 phân số bé nhất 1/18 và 2/13
tổng 1/18+2/13=49/234
tổng của 4 phân số Thăng và Long chọn là
49/12+49/234=2009/468
Cách 2 4 phân số mà Thăng và Long chọn là 1/18,2/13,7/3,7/4
tổng : 1/18+2/13+7/3+7/4=2009/468
nhé
Thăng chọn được hai phân số mà tổng có giá trị lớn nhất. Long chọn hai phân số mà tổng có giá trị nhỏ nhất. Tính tổng 4 số mà Thăng và Long đã chọn.
Bài giải:


Vậy ta sắp xếp được các phân số như sau :

Tổng hai phân số có giá trị lớn nhất là :

Tổng hai phân số có giá trị nhỏ nhất là:

Do đó tổng bốn phân số mà Thăng và Long đã chọn là:


Vậy ta sắp xếp được các phân số như sau:
Tổng hai phân số có giá trị lớn nhất là:
Tổng hai phân số có giá trị nhỏ nhất là:
Do đó tổng bốn phân số mà Thăng và Long đã chọn là:
\(\frac{7}{3}>\frac{7}{4}>\frac{7}{5}\)(1)
\(\frac{4}{5}>\frac{4}{13}\)(2)
\(\frac{4}{13}>\frac{2}{13}\)(3)
Từ (2) và (3) \(\Rightarrow\frac{4}{5}>\frac{4}{13}>\frac{2}{13}\)(4)
\(\frac{7}{5}>\frac{4}{5}\)(5)
Từ (1) (4) (5) \(\frac{7}{3}>\frac{7}{4}>\frac{7}{5}>\frac{4}{5}>\frac{4}{13}>\frac{2}{13}>\frac{1}{18}\)
\(\Rightarrow\frac{7}{3}+\frac{7}{4}+\frac{2}{13}+\frac{1}{18}=\)tự tính nột nhé


Input: dãy số nguyên gồm n số được nhập từ bạn phím
Output: số lớn nhất, bé nhất trong dãy
B1: nhập dãy số nguyên
B2: gán max:=a[1]; min:=a[1]
B3: nếu max<a[i] thì max:=a[i]; min>a[i] then min:=a[i]
B4: in kết quả ra màn hình

Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
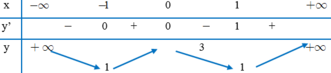
* Bước 3: Ta có bảng biến thiên sau:
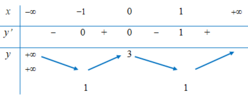
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.

Tọa độ đỉnh P là (-b/2a; -delta/4a)
với y=ax^2+bx+c
Áp dụng vào:
y=mx^2-(m+1)x-2m+3
Delta=(m+1)^2-4m(-2m+3)=m^2+2m+1+8m^2-12m=9m^2-10m+1
a=m,b=-(m+1),c=-2m+3
Là sẽ ra.
Để P(M) đi qua điểm (2,1)=> Thay x=2,y=1 vào cho cái đó =0
2=m-(m+1)-2m+3=>-2m+2=2=>m=0
y=mx^2-(m+1)x-2m+3
mx^2-mx-x-2m+3-y=0
=>m(x^2-x-2)-x-y+3=0
Điểm cố định có tọa độ (x_0,y_0)
Với x_0^2-x_0-2=0 và -x_0-y_0+3=0=>(x_0,y_0)=(2,-1) và (-1,-4)

c: include <bits/stdc++.h>
using namespace std;
long long a,b,c;
int main()
{
cin>>a>>b>>c;
cout<<max(a,max(b,c));
return 0;
}



Bài 13:
\(1)A=x^2-x+1\\ =\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{3}{4}\\ =\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\\ 2)B=x^2+x+1\\ =\left(x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{3}{4}\\ =\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\\ 3)C=x^2+2x+2\\ =\left(x^2+2x+1\right)+1\\ =\left(x+1\right)^2+1\ge1>0\forall x\)
\(4)A=x^2-5x+10\\ =\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}\right)+\dfrac{15}{4}\\ =\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}\ge\dfrac{15}{4}>0\forall x\\ 5)B=x^2-8x+20\\ =\left(x^2-8x+16\right)+4\\ =\left(x-4\right)^2+4\ge4>0\forall x\\ 6)C=x^2-8x+17\\ =\left(x^2-8x+16\right)+1\\ =\left(x-4\right)^2+1\ge1>0\forall x\)
\(7)A=x^2-6x+10\\ =\left(x^2-6x+9\right)+1\\ =\left(x-3\right)^2+1\ge1>0\forall x\\ 8)B=9x^2-6x+2\\ =\left(9x^2-6x+1\right)+1\\ =\left(3x-1\right)^2+1\ge1>0\forall x\\ 9)C=2x^2+8x+15\\ =\left(2x^2+8x+8\right)+7\\ =2\left(x^2+4x+4\right)+7\\ =2\left(x+2\right)^2+7\ge7>0\forall x\)