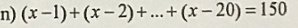
Giúp mình câu này ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DA
5
8 tháng 5 2016
2/7.x+20%.x=7/4
=> 2/7.x+1/5.x = 7/4
=> x. ( 2/7+1/5)=7/4
=> x . 17/35 = 7/4
=> x = 7/4 : 17/35
=> x = 1/340
8 tháng 5 2016
X = \(\frac{1}{340}\)
TÍCH MIK NHA 
Dương Anh Kiệt
HÃY TÍCH CHO MIK 1 TÍCH THÔI CŨNG ĐƯỢC
N
1
11 tháng 8 2015
\(\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+...+\frac{1}{x\cdot\left(x+2\right)}=\frac{20}{41}\)
\(\frac{1}{2}\cdot\left(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+\frac{2}{5\cdot7}+...+\frac{2}{x\cdot\left(x+2\right)}\right)=\frac{20}{41}\)
\(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}=\frac{20}{41}:\frac{1}{2}\)
\(1-\frac{1}{x+2}=\frac{40}{41}\)
\(\frac{1}{x+2}=1-\frac{40}{41}\)
\(\frac{1}{x+2}=\frac{1}{41}\)
\(\Rightarrow x+2=41\Rightarrow x=39\)
ML
7 tháng 8 2015
Hình như cần sửa thành \(\ge\)mới đúng
\(2x^2+xy+2y^2=\frac{1}{2}\left(x+y\right)^2+\frac{3}{2}\left(x^2+y^2\right)\ge\frac{1}{2}\left(x+y\right)^2+\frac{3}{2}.\frac{1}{2}\left(x+y\right)^2=\frac{5}{4}\left(x+y\right)^2\)
\(\Rightarrow\sqrt{2x^2+xy+2y^2}\ge\frac{\sqrt{5}}{2}\left(x+y\right)\)
\(\Rightarrow\sqrt{2x^2+xy+2y^2}+\sqrt{2y^2+yz+2z^2}+\sqrt{2z^2+zx+2x^2}\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\)
Dấu "=" xảy ra khi \(x=y=z=\frac{1}{3}\)
Vậy ta có đpcm.
9 tháng 3 2016
x/2 = 1/10 - 2/5
x/2 = 1/10 - 4/10
x/2 = (1 - 4)/10
x/2 = -3/10
x = (-3*2)/10
x = -6/10
x = -3/5
Vậy x = -3/5
Vì người ta ko nói x thuộc Z nên x là phân số đc.
Ủng hộ nha.
25 tháng 3 2017
a, A=4+2^2+2^3+...+2^20
2A=2(4+2^2+2^3+...+2^20)
2A=8+2^3+2^4+...+2^21
2A-A=(8+2^3+2^4+...+2^21)-(4+2^2+2^3+...+2^20)
A=2^21+8-4-2^2
A=2^21
Vay
LB
25 tháng 3 2017
a) A=\(2^{21}\)
b)
(x+1)+(X+2)+...+(x+100)=5750
=> 100x+(1+2+3+...+100)=5750
=> 100x+\(\frac{\left(100+1\right).100}{2}=5750\)
=> 100x+5050=5750
=>100x=700
=>x=7
AH
Akai Haruma
Giáo viên
23 tháng 10
Bạn lưu ý lần sau ghi đầy đủ yêu cầu đề bài.
Đề bài: Tìm nghiệm của đa thức.
AH
Akai Haruma
Giáo viên
23 tháng 10
Lời giải:
a/ $f(x)=2x-5=0$
$\Rightarrow 2x=5\Rightarrow x=\frac{5}{2}$
b/
$f(x)=x^2-25=0$
$\Rightarrow x^2=25=5^2=(-5)^2$
$\Rightarrow x=\pm 5$
c/
$f(x) = x^2+25=0$
$\Rightarrow x^2=-25<0$ (vô lý do $x^2\geq 0$ với mọi $x$)
Vậy đa thức này không có nghiệm.
d/
$f(x)=(x^2+1)(x-3)=0$
$\Rightarrow x^2+1=0$ hoặc $x-3=0$
$\Rightarrow x^2=-1$ (vô lý do $x^2\geq 0$ với mọi $x$) hoặc $x=3$ (chọn)
Vậy đa thức có nghiệm $x=3$
e/
$f(x)=x^2+x+1=(x^2+x+\frac{1}{4})+\frac{3}{4}$
$=(x+\frac{1}{2})^2+\frac{3}{4}\geq 0+\frac{3}{4}>0$ với mọi $x$
Do đó $f(x)\neq 0$ với mọi $x$
$\Rightarrow$ đa thức $f(x)$ không có nghiệm.
7 tháng 9 2015
ĐK x >= 0 ; y >=1 ; z >= 2
pt <=> \(2\sqrt{x}+2\sqrt{y-1}+2\sqrt{z-2}=x+y+z\)
=> \(x-2\sqrt{x}+1+y-1-2\sqrt{y-1}+1+z-2-2\sqrt{z-2}+1=0\)
=> \(\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\)
6 tháng 5 2021
\(\sqrt{x^2+4x+12}=2x-4+\sqrt{x+1}\) (1)
ĐKXĐ: x >= -1
Đặt x -2 = a; \(\sqrt{x+1}=b\)
Có \(x^2+4x+12=x^2-4x+4+8x+8=\left(x-2\right)^2+8\left(x+1\right)\)
=> \(\sqrt{x^2+4x+12}=\sqrt{\left(x-2\right)^2+8\left(x+1\right)}=\sqrt{a^2+8b^2}\)
(1) => \(\sqrt{a^2+8b^2}=2a+b\)
<=> \(\hept{\begin{cases}2a+b\ge0\\a^2+8b^2=\left(2a+b\right)^2\end{cases}}\)
<=> \(\hept{\begin{cases}2a+b\ge0\\3a^2+4ab-7b^2=0\end{cases}}\)
<=> \(\hept{\begin{cases}2a+b\ge0\\\left(a-b\right)\left(3a+7b\right)=0\end{cases}}\)
TH1: \(\hept{\begin{cases}2a+b\ge0\\a=b\end{cases}}\)
<=> \(\hept{\begin{cases}2a+b\ge0\\\sqrt{x+1}=x-2\end{cases}}\)
<=> \(\hept{\begin{cases}2\left(x-2\right)+\sqrt{x+1}\ge0\\x>2\\x+1=\left(x-2\right)^2\end{cases}}\)<=> \(x=\frac{5+\sqrt{5}}{2}\)
TH2: 3a+7b=0
Trường hợp 2 dài lắm nhưng cuối cùng kết quả vô nghiệm nhé!
P/s: mình không học đội tuyển toán nên mình cũng không biết cách này có được không nữa, mình chỉ làm theo cách cơ bản thôi! Bạn thông cảm nhé!
\(\left(x-1\right)+\left(x-2\right)+...+\left(x-20\right)=150\\ x-1+x-2+...+x-20=150\\ \left(x+x+...+x\right)-\left(1+2+...+20\right)\\ 20\cdot x-\left[\left(20-1\right):1+1\right]\cdot\left(20+1\right):2=150\\ 20\cdot x-20\cdot21:2=150\\ 20\cdot x-210=150\\ 20\cdot x=150+210\\ 20\cdot x=360\\ x=360:20\\ x=18\)