giúp tui zoiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2017
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].
- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
18 tháng 1 2022
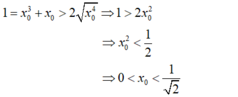
a:
Thay x=2 vào (1), ta được:
\(2^2-5\cdot2+6=0\)(đúng)
Thay x=2 vào (2), ta được:
\(2+\left(2-2\right)\cdot\left(2\cdot2+1\right)=2\)(đúng)
b: (1)=>(x-2)(x-3)=0
=>S1={2;3}
(2)=>\(x+2x^2+x-4x-2-2=0\)
\(\Leftrightarrow x^2+x-2=0\)
=>(x+2)(x-1)=0
=>S2={-2;1}
vậy: x=3 là nghiệm của (1) nhưng không là nghiệm của (2)
CM
9 tháng 11 2017
a) Thay x = 3 2 vào (1) và (2) thấy thỏa mãn nên x = 3 2 là nghiệm chung của cả hai PT đã cho.
b) Thay x = -5 vào (2) thấy thỏa mãn nên x = -5 là nghiệm của (2). Thay x = -5 vào (1) thấy không thỏa mãn nên x = -5 không là nghiệm của (1).
c) Cách 1. Tìm được tập nghiệm của (1) và (2) lần lượt là S 1 = { 1 ; 3 2 } và S 2 = { - 5 ; 3 2 }
Vì S 1 ≠ S 2 Þ Hai phương trình không tương đương nhau.
Cách 2. Theo ý b, x = -5 là nghiệm của (2) nhưng không là nghiệm của (1) nên hai PT không có cùng tập nghiệm.
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
a) Khi $m=1$ thì pt trở thành:
$x^2-2x-5=0$
$\Leftrightarrow (x-1)^2=6$
$\Rightarrow x=1\pm \sqrt{6}$
b) Để $x_1=3$ là nghiệm của pt thì:
$3^2-2.m.3+2m-7=0\Leftrightarrow m=\frac{1}{2}$
Nghiệm còn lại $x_2=(x_1+x_2)-x_1=2m-x_1=2.\frac{1}{2}-3=-2$
c)
$\Delta'= m^2-(2m-7)=(m-1)^2+6>0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm phân biệt $x_1,x_2$
Theo định lý Viet: $x_1+x_2=2m$ và $x_1x_2=2m-7$
Khi đó:
Để $x_1^2+x_2^2=13$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=13$
$\Leftrightarrow (2m)^2-2(2m-7)=13$
$\Leftrightarrow 4m^2-4m+1=0\Leftrightarrow (2m-1)^2=0\Leftrightarrow m=\frac{1}{2}$
d)
$x_1^2+x_2^2+x_1x_2=(x_1+x_2)^2-x_1x_2$
$=(2m)^2-(2m-7)=4m^2-2m+7=(2m-\frac{1}{2})^2+\frac{27}{4}\geq \frac{27}{4}$
Vậy $x_1^2+x_2^2+x_1x_2$ đạt min bằng $\frac{27}{4}$. Giá trị này đạt tại $m=\frac{1}{4}$
14 tháng 1 2022
a: \(\Delta=\left(m-3\right)^2-4\left(2m-1\right)\left(-6m-2\right)\)
\(=m^2-6m+9+4\left(2m-1\right)\left(6m+2\right)\)
\(=m^2-6m+9+4\left(12m^2+4m-6m-2\right)\)
\(=m^2-6m+9+48m^2-8m-8\)
\(=49m^2-14m+1=\left(7m-1\right)^2>=0\)
Vậy: Phương trình luôn có hai nghiệm
b: Các nghiệm của phương trình là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-m+3-7m+1}{2\left(2m-1\right)}=\dfrac{-8m+4}{2\left(2m-1\right)}=-2\\x_2=\dfrac{-m+3+7m-1}{2\left(2m-1\right)}=\dfrac{6m+2}{2\left(2m-1\right)}=\dfrac{3m+1}{2m-1}\end{matrix}\right.\)
CM
14 tháng 2 2017
Chọn D.
Phương trình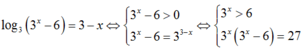 
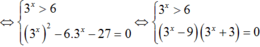
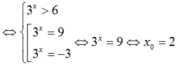
Mà x0 là nghiệm của phương trình log3( x + 7a) = 2log2x nên suy ra
log3( x + 7a) = 2log2x tương đương log3( x +7a) = 2
do đó; 7a + 2 = 32
suy ra a = 1.
NT
30 tháng 3 2018
tham khảo:https://www.vatgia.com/hoidap/5272/114204/toan-kho-lop-9-day--help.html
30 tháng 3 2018
ta có : ax=-(x^2+1)
bx=-(x^2+1)
abx=-(x^2+1)
=>ax=bx=abx
nếu x<>0 thi a=b=ab
=> a=b=1 => 4/(ab)^2 -1/a^2-1/b^2=2
nếu x=0 thi a=b=-1
thì 4/(ab)^2 -1/a^2-1/b^2=2
vậy 4/(ab)^2 -1/a^2-1/b^2=2
Nhận thấy \(x_0=0\) không phải là nghiệm của phương trình đã cho.
Giả sử \(x_0< 0\), ta có \(x_0^3-x_0-1=0\)
\(\Leftrightarrow x_0\left(x_0^2-1\right)=1\)
\(\Leftrightarrow x_0\left(x_0-1\right)\left(x_0+1\right)=1\) (*)
Nếu \(x_0\le-1\) thì VT (*) \(\le0< 1=VP\), do đó (*) vô lý.
Xét \(-1< x_0< 0\) thì \(-1< x_0^3< 0\) và \(0< -x_0< 1\)
Do đó \(VT=x_0^3-x_0< 0+1=1=VP\) nên (*) vô lý.
Vậy điều giả sử ban đầu là sai \(\Rightarrow x_0>0\)
Đặt f(x)=x3-x-1
Vì \(f\left(x\right)=x^3-x-1\)
nên hàm số liên tục trên R
\(f\left(1\right)=1^3-1-1=-1;f\left(2\right)=2^3-2-1=5\)
Vì \(f\left(1\right)\cdot f\left(2\right)< 0\)
nên hàm số f(x)=x3-x-1 có nghiệm trên khoảng (1;2)
=>\(x_0\in\left(1;2\right)\)
=>\(x_0>0\)