
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Tọa độ đỉnh P là (-b/2a; -delta/4a)
với y=ax^2+bx+c
Áp dụng vào:
y=mx^2-(m+1)x-2m+3
Delta=(m+1)^2-4m(-2m+3)=m^2+2m+1+8m^2-12m=9m^2-10m+1
a=m,b=-(m+1),c=-2m+3
Là sẽ ra.
Để P(M) đi qua điểm (2,1)=> Thay x=2,y=1 vào cho cái đó =0
2=m-(m+1)-2m+3=>-2m+2=2=>m=0
y=mx^2-(m+1)x-2m+3
mx^2-mx-x-2m+3-y=0
=>m(x^2-x-2)-x-y+3=0
Điểm cố định có tọa độ (x_0,y_0)
Với x_0^2-x_0-2=0 và -x_0-y_0+3=0=>(x_0,y_0)=(2,-1) và (-1,-4)




Giải
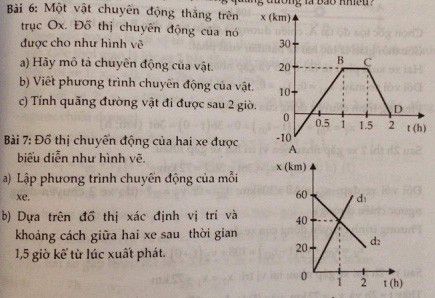
a. Phương trình chuyển động của hai xe
Xe ô tô: x1=30t
Xe mô tô: x2= 100 - 20t
b. Đồ thị toạ độ- thời gian, xác định
vị trí và thời điểm hai xe gặp nhau.
+ Chọn hệ toạ độ như hình vẽ:
+ Đồ thị toạ độ:
Của ô tô: Đoạn thẳng OM
Của mô tô: Đoạn thẳng PM
+ Vị trí hai xe gặp nhau: Cách gốc tạo độ 60km, thời
điểm hai xe gặp nhau là lúc 2h





Bài 2:
1: \(\dfrac{1}{5^{x-1}}+3\cdot5^{2-x}=\dfrac{16}{125}\)
=>\(\dfrac{1}{5^x\cdot\dfrac{1}{5}}+3\cdot\dfrac{25}{5^x}=\dfrac{16}{125}\)
=>\(\dfrac{5}{5^x}+\dfrac{75}{5^x}=\dfrac{16}{125}\)
=>\(\dfrac{80}{5^x}=\dfrac{16}{125}\)
=>\(5^x=80\cdot\dfrac{125}{16}=5\cdot125=5^4\)
=>x=4
2: \(\left(3-\left|x-\dfrac{1}{2}\right|\right)\left(\dfrac{8}{15}-\dfrac{1}{5}\right)+\dfrac{2}{3}=1\)
=>\(\left(3-\left|x-\dfrac{1}{2}\right|\right)\cdot\dfrac{1}{3}=1-\dfrac{2}{3}=\dfrac{1}{3}\)
=>\(3-\left|x-\dfrac{1}{2}\right|=1\)
=>\(\left|x-\dfrac{1}{2}\right|=3-1=2\)
=>\(\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2+\dfrac{1}{2}=\dfrac{5}{2}\\x=-2+\dfrac{1}{2}=-\dfrac{3}{2}\end{matrix}\right.\)
Bài 3:
1: Gọi ba phần được chia lần lượt là x,y,z
Ba phần tỉ lệ với 2/5;3/4;1/6 nên \(\dfrac{x}{\dfrac{2}{5}}=\dfrac{y}{\dfrac{3}{4}}=\dfrac{z}{\dfrac{1}{6}}\)
=>\(2,5x=\dfrac{4}{3}y=6z\)
=>\(15x=8y=36z\)
=>\(\dfrac{15x}{360}=\dfrac{8y}{360}=\dfrac{36z}{360}\)
=>\(\dfrac{x}{24}=\dfrac{y}{45}=\dfrac{z}{10}=k\)
=>x=24k; y=45k; z=10k
\(x^2+y^2+z^2=24309\)
=>\(\left(24k\right)^2+\left(45k\right)^2+\left(10k\right)^2=24309\)
=>\(k^2=9\)
=>\(\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
TH1: k=3
=>\(x=24\cdot3=72;y=45\cdot3=135;z=10\cdot3=30\)
TH2: k=-3
=>\(x=24\cdot\left(-3\right)=-72;y=45\cdot\left(-3\right)=-135;z=10\cdot\left(-3\right)=-30\)