Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

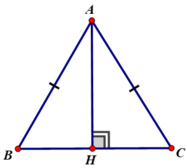
Xét hai tam giác vuông ΔABH và ΔACH đều vuông tại H có:
AB = AC (gt)
AH cạnh chung
Nên ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)
Suy ra HB = HC


tham khảo
a/ xét 2 tam giác vuông ABH và ACH,có:
AB=AC(gt),AH chung =>tam giác vuông ABH=tam giác vuông ACH
=>HB=HC(t/ứng
Xét 2 tam giác vuông ABH và ACH,có: AB=AC(gt),AH chung =>tam giác vuông ABH=tam giác vuông ACH =>HB=HC

xét 2 tam giác vuông ABH và ACH có
AH:cạnh chung
AB=AC(\(\Delta ABC\) cân tại A)
do đó \(\Delta ABH=\Delta ACH\)(cạnh huyền-góc nhọn)
suy ra HB=HC(2 cạnh tương ứng)

* Vẽ hình hộ mình nha !!!
a) Xét tam giác ABH và tam giác ACH vuông tại H có:
+) AB = AC (chứng minh trên)
+) Góc B = góc C (cmt)
=> Tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn)
=> HB = HC (2 cạnh tương ứng)
b) Vì tam giác ABH = tam giác ACH nên:
=> Góc BAH = góc CAH (2 góc tương ứng)
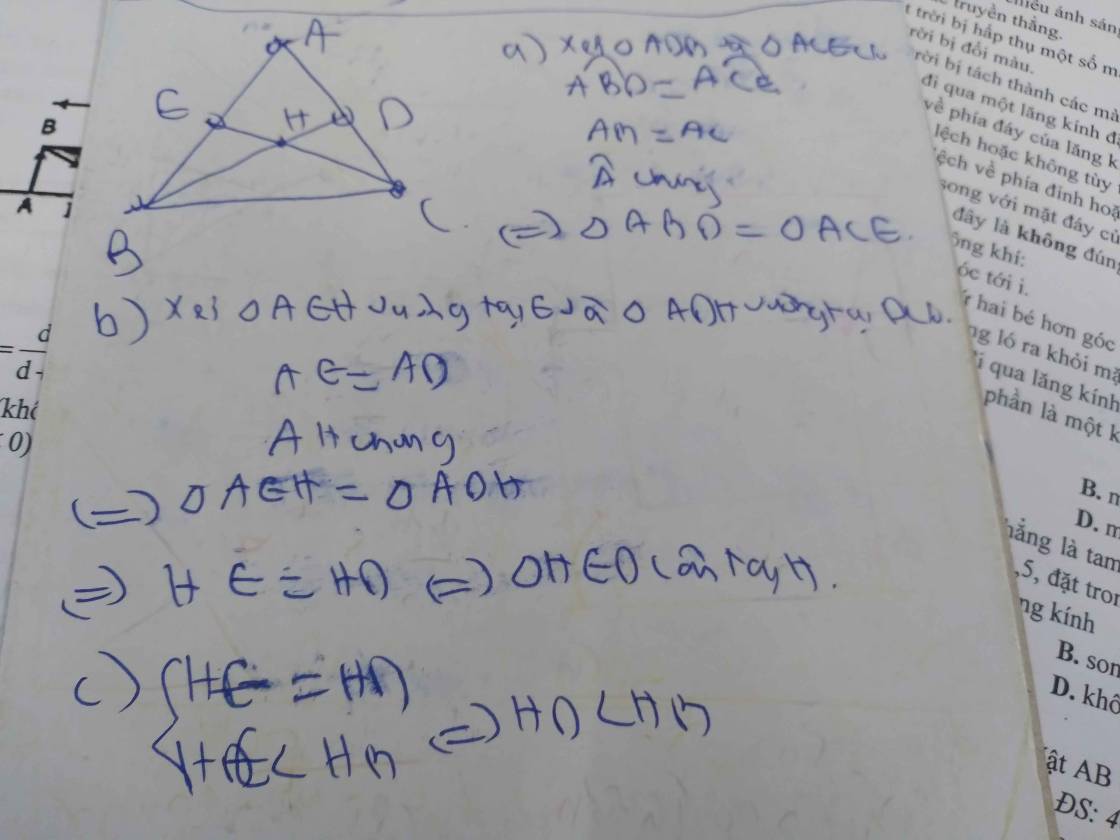
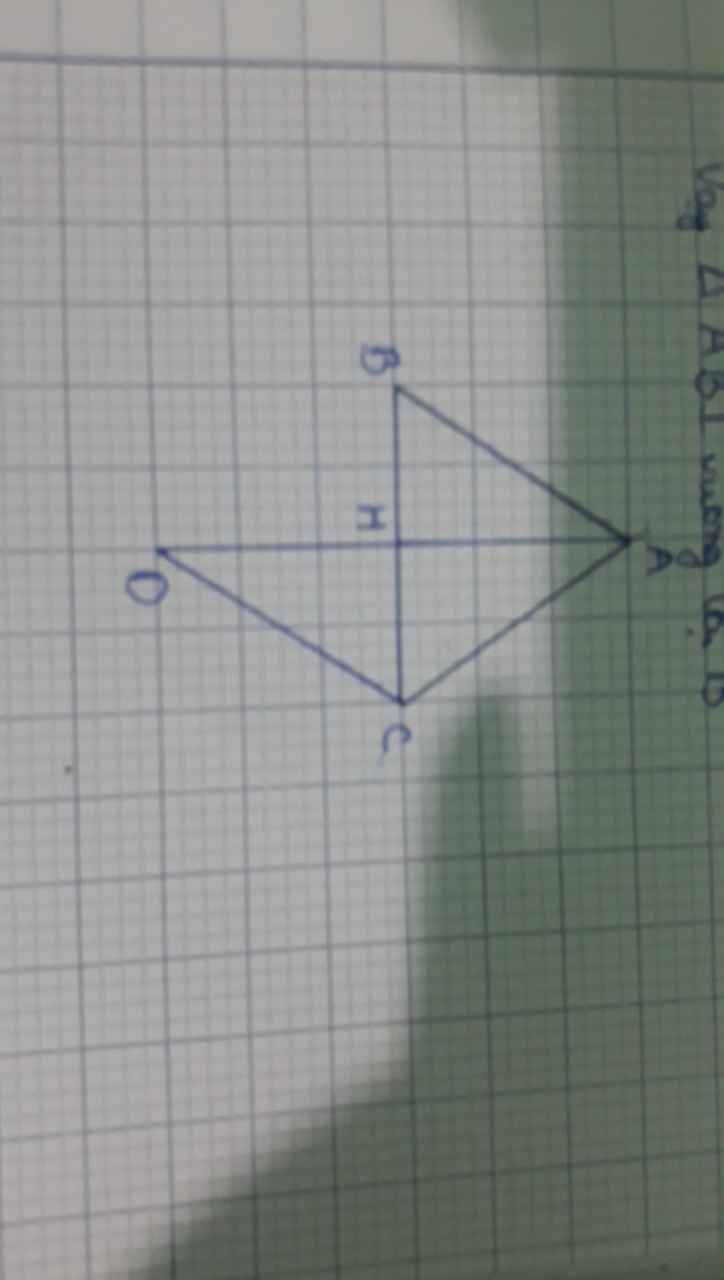

Xét ΔABC có
HB,HC lần lượt là hình chiếu của AB,AC trên BC
AB=AC
Do đó: HB=HC