Mn giúp em bài hình với 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 11 2021
Bài 1: hình 2:
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow20x=144\Rightarrow x=\dfrac{36}{5}\)
\(x+y=BC\Rightarrow\dfrac{36}{5}+y=20\Rightarrow y=\dfrac{64}{5}\)
Bài 2:
hình 4:
BC=BH+HC=1+4=5
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow1.5=AB^2\Rightarrow x=\sqrt{5}\)
áp dụng HTL ta có: \(HC.BC=AC^2\Rightarrow4.5=AC^2\Rightarrow y=2\sqrt{5}\)
hình 6:
Áp dụng HTL ta có: \(BH.HC=AH^2\Rightarrow4x=25\Rightarrow x=\dfrac{25}{4}\)
TL
1
26 tháng 10 2021
Bài 1:
a: \(36a^4-y^2=\left(6a^2-y\right)\left(6a^2+y\right)\)
n: \(6x^2+x-2\)
\(=6x^2+4x-3x-2\)
\(=\left(3x+2\right)\left(2x-1\right)\)
L2
2
HN
1
26 tháng 8 2021
a: Xét ΔIMC vuông tại I và ΔINC vuông tại I có
IM=IN
CI chung
Do đó: ΔIMC=ΔINC
b: Xét ΔCKB có
M là trung điểm của BC
MN//KB
Do đó: N là trung điểm của CK
8 tháng 9 2021
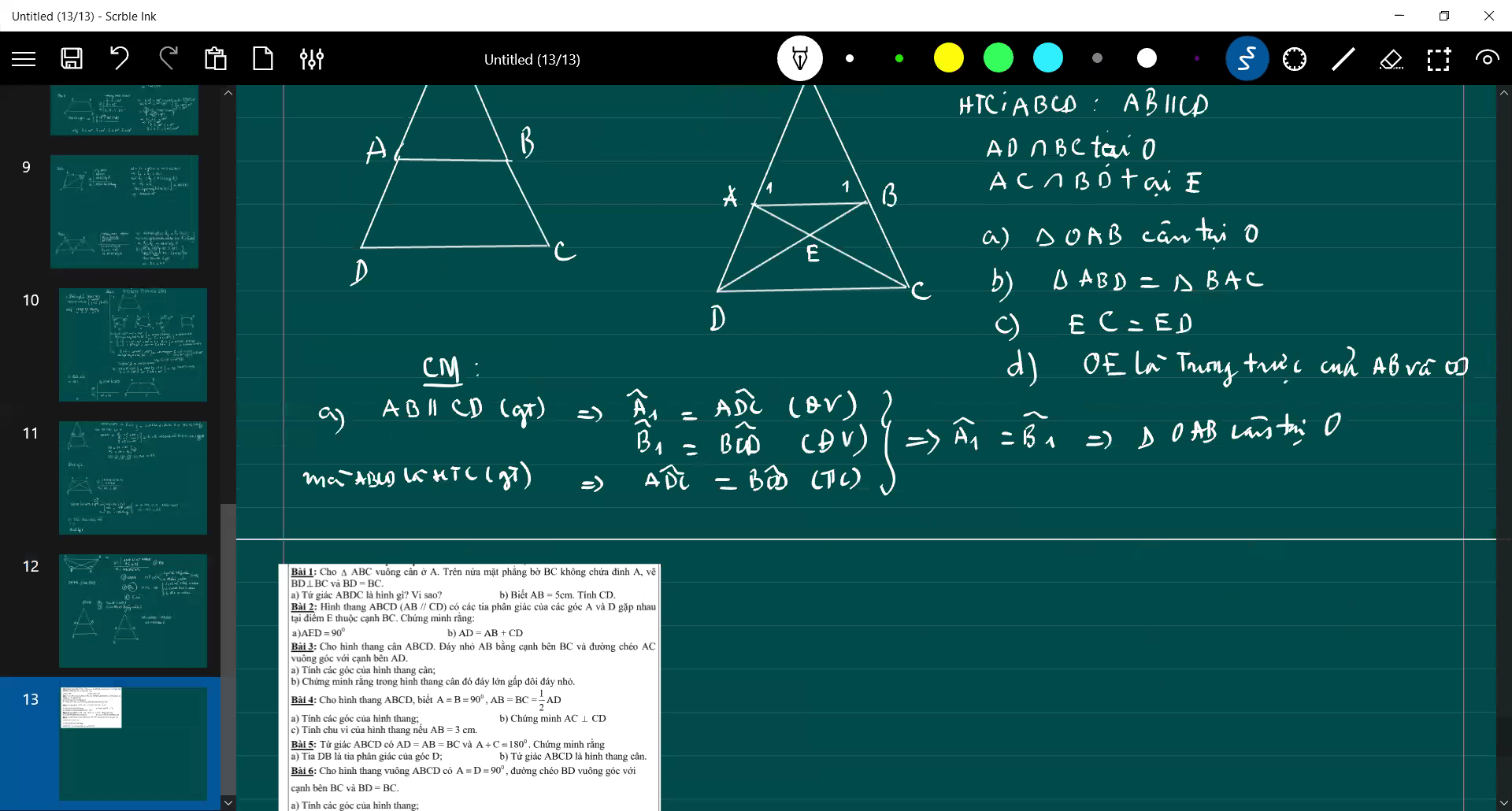
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
BT
5 tháng 9 2023
Những hình ảnh được nhắc đến trong bài hát Khai trường là: Lớp học, bạn bè, sân trường, thầy cô, áo trắng, khăn đỏ, vở mới.
Em ấn tượng với hình ảnh : ... vd: khăn quàng đỏ tung trong gió tượng như ... cái j đó bn tự nghĩ nha .( theo ý bn tự nói ra ấn tượng của bài )
Mog mik giúp còn kịp cho bn 
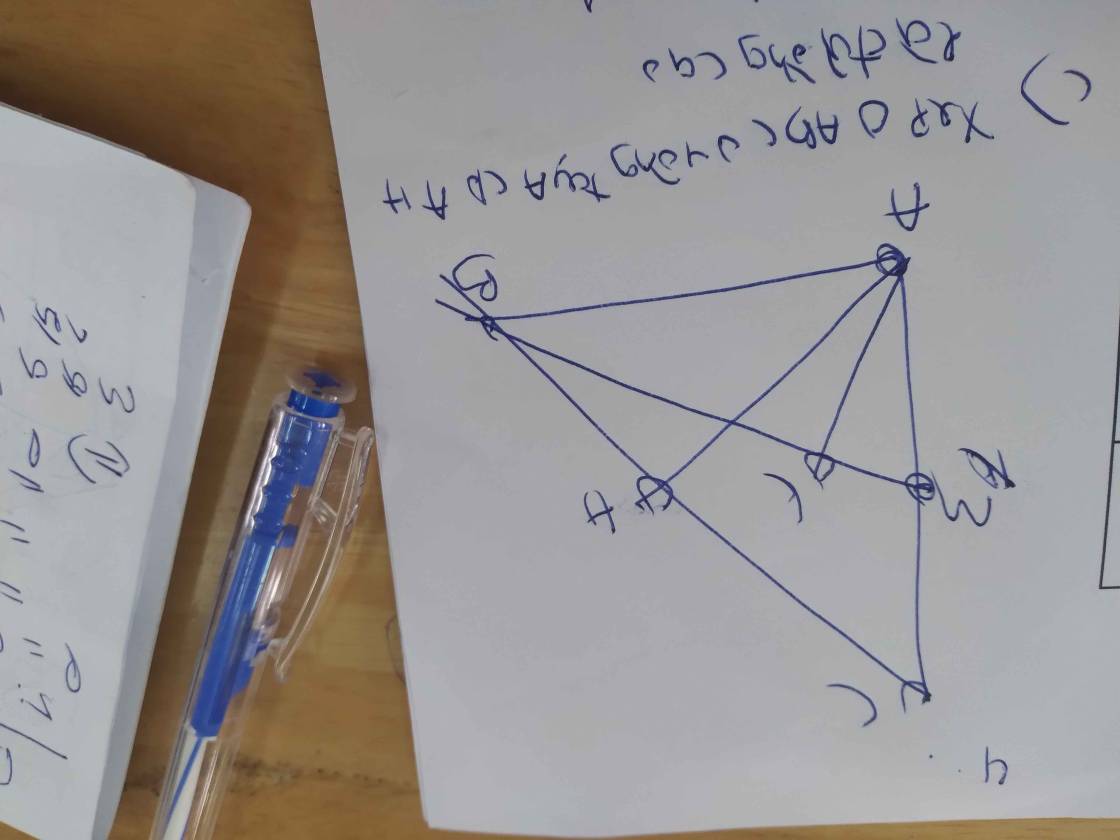
ta có: \(\widehat{ABM}+\widehat{ABC}=180^o\)(2 góc kề bù)
Mặc khác:
\(\widehat{ACN}+\widehat{ACB}=180^o\)(2 góc kề bù)
Mà \(\widehat{ABC}=\widehat{ACB}\) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
xét ΔABM và ΔACN có:
AB=AC(ΔABC cân tại A)
BM=CN(gt)
\(\widehat{ABM}=\widehat{ACN}\)(ch/m trên)
⇒ΔABM=ΔACN(c-g-c)
⇒AM=AN(2 cạnh tương ứng)
⇒ΔAMN cân(đ.p.ch/m)
xét ΔECN và ΔBDM có:
\(\widehat{MDB}=\widehat{NEC}=90^o\)
BM=CN(gt)
\(\widehat{DMB}=\widehat{ENC}\)(ΔABM=ΔACN)
⇒ΔECN=ΔBDM(c.huyền.g.nhọn)
⇒BD=CE(2 cạnh tương ứng)
a) Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
b) Xét ΔDMB vuông tại D và ΔENC vuông tại E có
BM=CN(gt)
\(\widehat{DMB}=\widehat{ENC}\)(ΔAMB=ΔANC)
Do đó: ΔDMB=ΔENC(cạnh huyền-góc nhọn)
Suy ra: BD=CE(hai cạnh tương ứng)