Cho tam giác ABC, góc A = 700 , góc C = 400 . Trên nửa mặt phẳng bờ AB có chứa C vẽ tia Ax sao cho góc Bax = 1100 . Chứng tỏ rằng tia Ax // BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


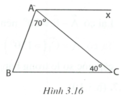
Tia AC nằm giữa hai tia AB và Ax nên B A C ^ + C A x ^ = B A x ^
⇒ C A x ^ = 110 ° − 70 ° = 40 ° .
Do đó C A x ^ = C ^ = 40 ° .
Suy ra Ax // BC vì có cặp góc so le trong bằng nhau

a, ta có : BAx = 1300
ABD = 500
-> BAx + ABD = 1300 + 500 = 1800
=> BAx và ABD là cặp góc cùng phía bù nhau
=> Ax // BD
b, Ax // BD => C1 = A45 ( So le trong )
=> C1 + A3 = A45 + A3 = A345 = 1300
Góc B = 50 độ
Vậy B + C1 + A3 = 180 độ
=> Tổng 3 góc trong tam giác ABC = 1800
c, A12345 = 180 0
A345 = 1300
=> A12 = 500
AF là phân giác của A12 => A1 = A2 = 500/2 = 250
AD là phân giác của A345 => A34 = A5 = 650
=> A3 + A34 = 250 + 650 = 900
ta có : FAD = 900
=> AF vuông góc với AC

giải thích một số từ viết tắt:tam giác(tg) , góc (g)
TH1: tia Ax và AC nằm ở 2 nửa mặt phẳng đối nhau bờ là BA. CÒn tia Ay và AB nằm 2 nwả mặt phẳng bờ đối nhau bờ là AC:
TRên tia MA lấy điểm I sao cho MI=MA. tg BAM=tg CIM(c.g.c) => g ABM=gMCI=> gACI=gACM+gBAM=180- g BAC và BA=CI
LẠi có gDAE=180-gBAC nên gACI=gDAE. Dễ dàng chứng minh được tgACI=tgEAD(c.g.c)=>DE=AI=2AM
TH2: tia Ax và AC nằm cùng phía đối với BA. Còn BA và AE cùng phía đối với AC.trên tia đối MA lấy K sao cho KM=KA
Kéo dài BC nó sẽ cắt EA ở I gEAB= gABC-gAIB=gABC-90-gACB . tg EAB=tgCAD(c.g.c)=>gEAB+gDAC
TA có : gEAD=(gEAB+gDAC)+gBAC=(gABC-90-gACB)2+(1... =gB+gC=gBCK+gACM=gACK.Chứng minh tg ACK=tgEAD(c.g.c)=>AK=ED=2AM.
Cho tam giác ABC vuông góc tại B. trên cùng nửa mặt phẳng bờ chứa tia AC chứa điểm B vẽ tại tia Ax, Cy sao cho góc xAB=30 độ ,góc BCy=60 độ. Tìm kết luận
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{B}+70^0+40^0=180^0\)
=>\(\widehat{B}=70^0\)
Ta có: \(\widehat{xAB}+\widehat{ABC}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ax//BC