ae cứu tôi giải hệ phương trình
x+2y=1+3
2x-3y=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 2 2019
Câu 1: ĐK: x khác -1/2, y khác -2
Đặt \(\sqrt[3]{\frac{2x+1}{y+2}}=t\) Từ phương trình thứ nhất ta có:
\(t+\frac{1}{t}=2\Leftrightarrow t^2-2t+1=0\Leftrightarrow t=1\)
=> \(\sqrt[3]{\frac{2x+1}{y+2}}=1\Leftrightarrow2x+1=y+2\Leftrightarrow2x-y=1\)
Vậy nên ta có hệ phương trình cơ bản: \(\hept{\begin{cases}2x-y=1\\4x+3y=7\end{cases}}\)Em làm tiếp nhé>
21 tháng 2 2019
\(1,ĐKXĐ:\hept{\begin{cases}y\ne-2\\x\ne-\frac{1}{2}\end{cases}}\)
Đặt \(\sqrt[3]{\frac{2x+1}{y+2}}=a\left(a\ne0\right)\)
\(Pt\left(1\right)\Leftrightarrow a+\frac{1}{a}=2\)
\(\Leftrightarrow a^2+1=2a\)
\(\Leftrightarrow\left(a-1\right)^2=0\)
\(\Leftrightarrow a=1\)
\(\Leftrightarrow\sqrt[3]{\frac{2x+1}{y+2}}=1\)
.
18 tháng 5 2022
1: Khi m=3 thì hệ phương trình (1) trở thành:
\(\left\{{}\begin{matrix}3x-2y=-1\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{13}\\y=\dfrac{5}{13}\end{matrix}\right.\)
2: Khi x=-1/2 và y=2/3 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2\cdot\dfrac{-1}{2}+3\cdot\dfrac{2}{3}=1\\-\dfrac{1}{2}m-\dfrac{4}{3}=-1\end{matrix}\right.\Leftrightarrow m\cdot\dfrac{-1}{2}=\dfrac{1}{3}\)
hay m=-2/3
6 tháng 4 2023
1: =>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=1 hoặc x=-4
2: =>2x-3y=1 và 3x=4y+2
=>2x-3y=1 và 3x-4y=2
=>x=2 và y=1
KS
1
16 tháng 5 2017
\(\hept{\begin{cases}x^3+2x=y^3+2y\left(1\right)\\x^2+3y^2=1\left(2\right)\end{cases}}\)
Xét PT (1) ta có:
\(x^3-y^3+2x-2y=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2+2\right)=0\)
Vì \(x^2+xy+y^2+2>0\) nên
\(\Rightarrow x=y\)
Thế vô PT (2) ta có
\(4x^2=1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
CM
7 tháng 2 2017
a) Điều kiện x ≥ 1; y ≥ 1.
Đặt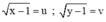 
(u, v ≥ 0).
Hệ phương trình trở thành:
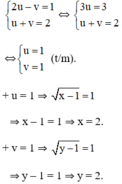
Vậy hệ phương trình có nghiệm (2; 2).
b) Đặt (x – 1)2 = u, u ≥ 0.
Hệ phương trình trở thành:
u − 2 y = 2 3 u + 3 y = 1 ⇔ 3 u − 6 y = 6 3 u + 3 y = 1 ⇔ − 9 y = 5 u − 2 y = 2 ⇔ y = − 5 9 u = 8 9 + u = 8 9 ⇒ ( x − 1 ) 2 = 8 9 ⇔ x − 1 = 2 2 3 x − 1 = − 2 2 3 ⇔ x = 2 2 + 3 3 x = − 2 2 + 3 3
Vậy hệ phương trình có hai nghiệm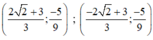 
CM
6 tháng 4 2017
a) Điều kiện x ≥ 1; y ≥ 1.
Đặt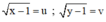 
(u, v ≥ 0).
Hệ phương trình trở thành:
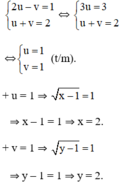
Vậy hệ phương trình có nghiệm (2; 2).
b) Đặt ( x – 1 ) 2 = u , u ≥ 0.
Hệ phương trình trở thành:
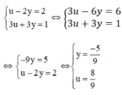
Vậy hệ phương trình có hai nghiệm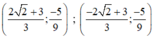 
\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\7y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2=4\\y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4-2=2\\y=1\end{matrix}\right.\)
Vậy: ...
\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-\left(2x-3y\right)=8-1\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-2x+3y=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\\left(2x-2x\right)+\left(4y+3y\right)=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\0+7y=7\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\y=1\end{matrix}\right.\)
Thay y = 1 vào biểu thức 2\(x\) + 4y = 8 ta có: 2\(x\) + 4.1 = 8
⇒ 2\(x\) + 4 = 8 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 ⇒ \(x\) = 2
Vậy \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)