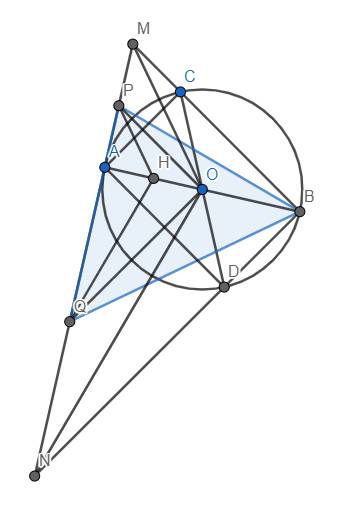
Cho 2 đường tròn đồng tâm với các bán kính là \(R\) và \(R_1\) \(\left(R>R_1\right)\) và một tứ giác lồi ABCD nội tiếp đường tròn nhỏ. Các tia AB, BC, CD và DA lần lượt cắt đường tròn lớn tại C1, D1, A1, B1. Chứng minh rằng:
(i) \(\dfrac{C_{A_1B_1C_1D_1}}{C_{ABCD}}\ge\dfrac{R_1}{R}\) với \(C_X\) là chu vi của X
(ii) \(\dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}\ge\left(\dfrac{R_1}{R}\right)^2\) với \(S_X\) là diện tích của X