xác định dạng của tam giác abc,biết: ab= 15cm,bc=20cm,ac=25cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ AH vuông góc với BC
Ta có: AB2+AC2=152+202=625
BC2=252=625
=>Tam giác ABC vuông tại A
=> SABC=AB.AC/2 hoặc SABC=AH.BC/2
=>AB.AC/2=AH.BC/2
=>AB.AC=AH.BC
=>15.20=AH.25
=>AH=12
Vậy k/c cần tìm là 12 cm


\(a,AB^2+AC^2=15^2+20^2=625=25^2=BC^2\)
Vậy ABC là tam giác vuông tại A (pytago đảo)
\(b,\)Áp dụng HTL tam giác ABC vuông tại A, đường cao AH
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9\left(cm\right)\\CH=\dfrac{AC^2}{BC}=12\left(cm\right)\\AH=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Vì AM là phân giác nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow MB=\dfrac{3}{4}MC\)
Mà \(MB+MC=BC=25\Rightarrow\dfrac{7}{4}MC=25\)
\(\Rightarrow MC=\dfrac{100}{7}\left(cm\right);MB=\dfrac{75}{7}\left(cm\right)\)

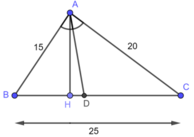
Xét t/gABC ta thấy AD là đường p/g của BAC
=>DB/DC=AB/AC (t/c phân giác)
Mà AB=15 cm ;AC=20cm nên ta có:
DB/DC=15/20
=> ta có tỉ lệ thức sau: DB/DB+DC=15/15+20 (t/c tỉ lệ thức)
=>DB/BC=15/35=>DB=15/35.BC=15/35.25=75/7(cm).
b) Ta kẻ AH _|_ BC
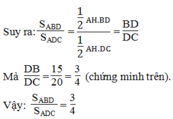
=>SABD=1/2AH.BD
=>SACD=1/2AH.DC
=>SABD/SACD=1/2AH.BD/1/2AH.DC=BD/DC
Mà ta thấy DB/DC=15/20=3/4
=> t/s SABD và SACD=3/4.
P/S: Bài này mik làm rồi nên hình mũi tên chỉ điển hình AB=15cm AC..... thôi nhé :< Cậu đừng ghi vào cũng được

a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)
Ta có: AC > BC > AB
\(BC^2+AB^2=20^2+15^2=625\) (1)
\(AC^2=25^2=625\) (2)
Từ (1) và (2) \(\Rightarrow BC^2+AB^2=AC^2\)
Vậy ΔABC là tam giác vuông tại C
Ta có:
\(\left\{{}\begin{matrix}AB=15\left(cm\right)\\BC=20\left(cm\right)\\AC=25\left(cm\right)\end{matrix}\right.\)(giả thiết)
\(\Rightarrow\left\{{}\begin{matrix}AB^2+BC^2=15^2+20^2=225+400=625\left(cm\right)\\AC^2=25^2=625\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow AB^2+BC^2=AC^2\)
\(\Rightarrow\Delta ABC\) vuông (theo định lý Pi-ta-go đảo)
Vậy \(\Delta ABC\) là tam giác vuông.