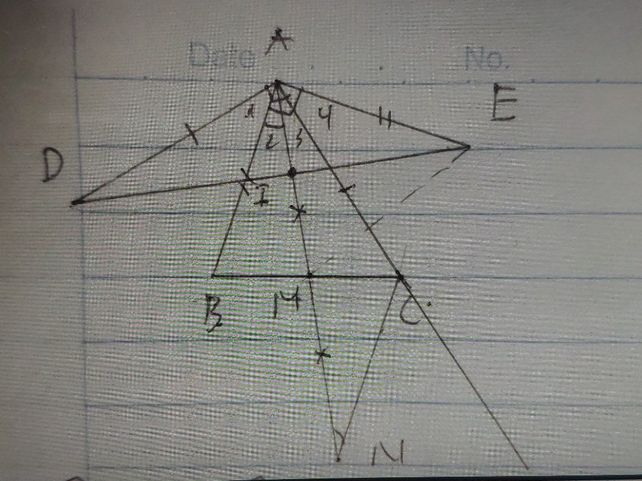
Cho 3 điểm A, B, C sao cho AB = AC, Vẽ \(\Delta ADE\) sao cho AC là đường cao. Tìm GTNN của \(\dfrac{1}{AD^2}\)+\(\dfrac{1}{AE^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2022
a: AE/AD=9/6=3/2
AB/AC=8/12=2/3
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
Do đó:ΔADE đồng dạng với ΔABC
HQ
4 tháng 7 2017
Các bạn Đoàn Đức Hiếu; Nguyễn Huy Tú; Akai Haruma; Hà Linh; Ace Legona;... LÀM ƠN GIÚP MÌNH ĐI MÀ!!!
DT
17 tháng 2 2022
có không hiểu chỗ nào thì hỏi lại nhoa:33
theo đề ta sẽ có : \(S_{ABC}=\dfrac{AB.AC}{2}=20\left(m^2\right)\)(1)
thì tương tự ta sẽ có : \(S_{ADE}=\dfrac{AD.AE}{2}=..\)
mà \(AD=\dfrac{1}{3}AB;AE=\dfrac{3}{5}AC\)
thay vào (1) ta có : \(S_{ADE}=\dfrac{\dfrac{1}{3}AB.\dfrac{3}{5}AC}{2}=....\)
cũng từ (1) ta suy ra được : AB . AC = 40 (m)
vậy giờ ta có : \(S_{ADE}=\dfrac{\dfrac{1}{5}.40}{2}=4\left(m^2\right)\)
3 tháng 2 2019
tu ve hinh :
a, AE | AB va AD | AC (gt) => goc DAC = goc BAE = 90 (dn)
goc DAB + goc BAC = goc DAC
goc EAC + goc CAB = goc BAE
=> goc DAB = goc CAE
xet tamgiac BDA va tamgiac ECA co :
AD = AC (gt) va AB = AE (gt)
=> tamgiac BDA = tamgiac ECA (c - g - c)
=> BD = CE (dn)