Cho khối lăng trụ tam giác đều ABC A' B' C' có cạnh đáy bằng 2a . Gọi M là trung điểm BC . Biết khoảng cách giữa hai đường thẳng A' B và C' M bằng a/2. Thể tích khối lăng trụ đã cho bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là B.
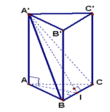
Gọi I là trung điểm BC.
Ta có Δ A B C đều nên A I = A B 3 2 = 2 3 .
A I ⊥ B C A A ' ⊥ B C ⇒ A ' I ⊥ B C
S A ' B C = 1 2 B C . A ' I ⇒ A ' I = 2 S A ' B C B C = 4
A A ' ⊥ ( A B C ) ⇒ A A ' ⊥ A I .
Xét Δ A ' A I vuông tại ⇒ A A ' = A ' I 2 − A I 2 = 2
Vậy V A B C . A ' B ' C ' = S A B C . A A ' = 4 2 3 4 .2 = 8 3

Chọn D
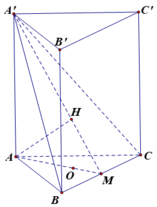
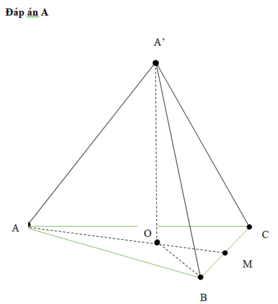
Gọi M là trung điểm của BC và H là hình chiếu của A trên A'M.
Ta có :
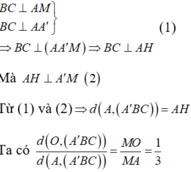
(do tính chất trọng tâm).

Xét tam giác vuông A'AM :
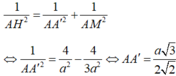
Suy ra thể tích lăng trụ ABC. A'B'C' là:


Chọn D
Diện tích đáy là B = S ∆ A B C = a 2 3 4 .
Chiều cao là h = d((ABC); (A'B'C')) = AA'
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC. Gọi I là trung điểm của BC, H là hình chiếu vuông góc của A lên A'I ta có:
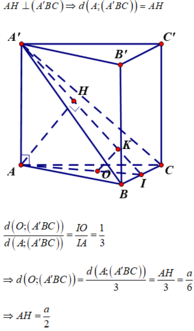
Xét tam giác A'AI vuông tại A ta có:
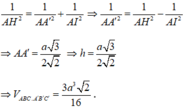

Đáp án A
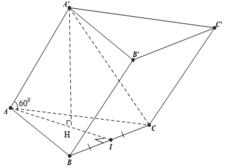
Gọi I là giao điểm của AH và BC
Theo giả thiết H là trực tâm của tam giác đều ABC nên AH là đường cao và H cũng lả trọng tâm của tam giác đều ABC


Đáp án C
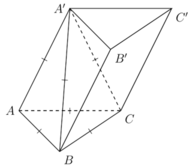
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là
V A ' A B C = a 3 2 12
Khi đó
V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4

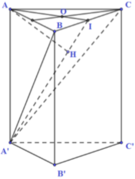
Gọi I là trung điểm của BC, kẻ A H ⊥ A ' I
∆
A
B
C
đều cạnh 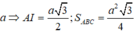
Ta có: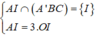
![]()
Ta có: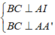
![]()
Mà ![]()
![]()
![]()
⇒ A H 2 = a 2
∆ A A ' I vuông tại A, A H ⊥ A ' I
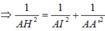
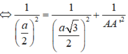
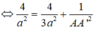
Thể tích khối lăng trụ ABCD.A'B'C'D là: V = S ∆ A B C . A A '
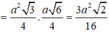
Chọn đáp án A.
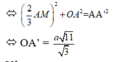


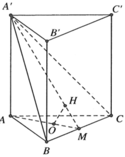
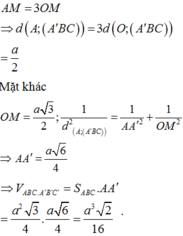
Chọn hệ trục tọa độ Mxyz (M là gốc tọa độ) sao cho Mx trùng với tia MB, My trùng với tia MA và Mz cùng phương với BB' sao cho \(\overrightarrow{BB'}\) hướng theo chiều dương của Mz.
Gọi chiều cao lăng trụ là \(h>0\)
Khi đó \(B\left(a;0;0\right)\), \(C'\left(-a;0;h\right)\), \(A'\left(0;a\sqrt{3};h\right)\)
Ta có \(\overrightarrow{MC'}=\left(-a;0;h\right),\overrightarrow{BA'}=\left(-a;a\sqrt{3};h\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]=\left(-ah\sqrt{3};0;a^2\sqrt{3}\right)\)
\(\Rightarrow\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|=\sqrt{\left(-ah\sqrt{3}\right)^2+\left(a^2\sqrt{3}\right)^2}=a\sqrt{3h^2+3a^2}\)
Lại có \(\overrightarrow{MB}=\left(a;0;0\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}=-a^2h\sqrt{3}\)
\(\Rightarrow d\left(MC',BA'\right)=\dfrac{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}\right|}{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|}\) \(=\dfrac{a^2h\sqrt{3}}{a\sqrt{3a^2+3h^2}}=\dfrac{ah}{\sqrt{a^2+h^2}}\)
Theo đề bài, ta có: \(\dfrac{ah}{\sqrt{a^2+h^2}}=\dfrac{a}{2}\)
\(\Leftrightarrow\dfrac{h}{\sqrt{a^2+h^2}}=\dfrac{1}{2}\)
\(\Leftrightarrow2h=\sqrt{a^2+h^2}\)
\(\Leftrightarrow4h^2=a^2+h^2\)
\(\Leftrightarrow3h^2=a^2\)
\(\Leftrightarrow h=\dfrac{a}{\sqrt{3}}\)
\(\Rightarrow V=S_đ.h=\dfrac{\left(2a\right)^2\sqrt{3}}{4}.\dfrac{a}{\sqrt{3}}=a^3\)
Vậy thể tích lăng trụ bằng \(a^3\)