chứng tỏ rằng hai tia phân giác của 2 góc kề bù vuông góc với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét các tia x'ox và y'oy, có hai góc đối đỉnh là xoy và x'oy'
gọi ot và ot' là hai tia phân giác tương ứng
Thấy: góc xoy = góc x'oy'
=> góc yot = góc y'ot'
Ta có: góc xoy + góc xoy' = góc toy' + góc yot = 180o
<=> góc toy' + góc y'ot' = góc tot' = 180o
=> ot và ot' là hai tia đối nhau.
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

Cho góc AOB và góc BOC là hai góc kề bù , OM , ON lần lượt là các ia phân giác của góc ACB và góc BOC
Chứng minh góc MON = 90 độ
Ta có : OM là tia phân giác của góc AOB nên tia OM nằm giữa hai tia OA và OB và góc MOB = 1/2 góc AOB
Tương tự : ON là tia pân giác của góc BOC nên ON nằm giữa hai tia OB và OC và góc BON = 1/2 góc BOC
Lại có : góc AOB và góc BOC là hai góc kề bù nên tia OB nằm giữa hai tia OA va OC
Suy ra : OB nằm giữa hai tia OM và ON nên :
góc MON = góc MOB + góc BON
= 1/2 * ( góc AOB + góc BOC )
= 1/2 * 180 độ = 90 độ
Cho góc AOB và góc BOC là hai góc kề bù , OM , ON lần lượt là các ia phân giác của góc ACB và góc BOC Chứng minh góc MON = 90 độ Ta có : OM là tia phân giác của góc AOB nên tia OM nằm giữa hai tia OA và OB và góc MOB = 1/2 góc AOB Tương tự : ON là tia pân giác của góc BOC nên ON nằm giữa hai tia OB và OC và góc BON = 1/2 góc BOC Lại có : góc AOB và góc BOC là hai góc kề bù nên tia OB nằm giữa hai tia OA va OC Suy ra : OB nằm giữa hai tia OM và ON nên : góc MON = góc MOB + góc BON = 1/2 * ( góc AOB + góc BOC ) = 1/2 * 180 độ = 90 độ

Tham khảo link này nhé ^^
https://h7.net/hoi-dap/toan-7/hai-tia-phan-giac-cua-hai-goc-ke-bu-vuong-goc-voi-nhau-faq25757.html

\(Góc\)\(kề\)\(bù\)\(có\)\(số\)\(đo=90^0\)
\(2\)\(góc\)\(kề\)\(bù\)\(\Rightarrow mỗi\)\(góc=90^0\)
\(Tia\)\(phân\)\(giác\)\(của\)\(1\)\(góc\)\(kề\)\(bù=90^0:2=45^0\)
\(\Rightarrow Tia\)\(phân\)\(giác\)\(của\)\(2\)\(góc\)\(kề\)\(bù=45^0+45^0=90^0\)
thấy: xOy + yOz = 1800
=>1/2 xOy + 1/2 yOz = 1/2(xOy+yOz)=1/2 xOz=1/2 x 180 dộ
=90 độ
Vậy hai tia phân giác của 2 góc kề bù thì vuông góc với nhau

Xét Om và On thứ tự là tia phân giác của hai góc kề bù x O z ^ và z O y ^ . Ta có: x O z ^ + z O y ^ = 180 0 (hai góc kề bù) Mà Om là tia phân giác của x O z ^ => x O z ^ = 2 m O z ^ On là tia phân giác của z O y ^ ⇒ z O y ^ = 2 n O z ^ |
|
Do đó: 2 m O z ^ + 2 n O z ^ = 180 0
⇒ m O z ^ + n O z ^ = 90 0
⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n
Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau

* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

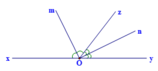
Ta có hình vẽ sau
Gỉa sử góc xOz=120 độ thì tia phân giác Om sẽ chia ra hai góc 60 độ
Góc yOz=60 độ thì tia phân giác On sẽ chia hai góc 30 độ
Cộng hai góc với nhau sẽ có 1 góc 90 độ là 1 góc vuông
Nên tia phân giác của hai góc kề bù luôn vuông góc với nhau
bn vẽ hình từ trái qua phải nhé:vẽ đt :xOy,Oz nằm giữa 2 tia Oy,Ox;Oz là tia pg của góc xOt;Oh là tia pg của tOy
ta có:
góc xOt + tOy = 180(độ)
=>2zOt+2tOh=180(độ)
=>2(zOt+tOh)=180(độ)
=>zOt+tOh=180:2=90
=>tia Oz vuông góc vs tia Oh
=> 2 tia pg của 2 góc kề bù vuông góc vs nhau
Gọi hai góc kề bù là góc AOC và góc BOC, gọi OD,OE lần lượt là phân giác của góc AOC và góc BOC
OD là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{COD}\)
OE là phân giác của góc BOC
=>\(\widehat{BOC}=2\cdot\widehat{EOC}\)
Ta có: \(\widehat{AOC}+\widehat{BOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{COD}+\widehat{COE}\right)=180^0\)
=>\(2\cdot\widehat{DOE}=180^0\)
=>\(\widehat{DOE}=90^0\)