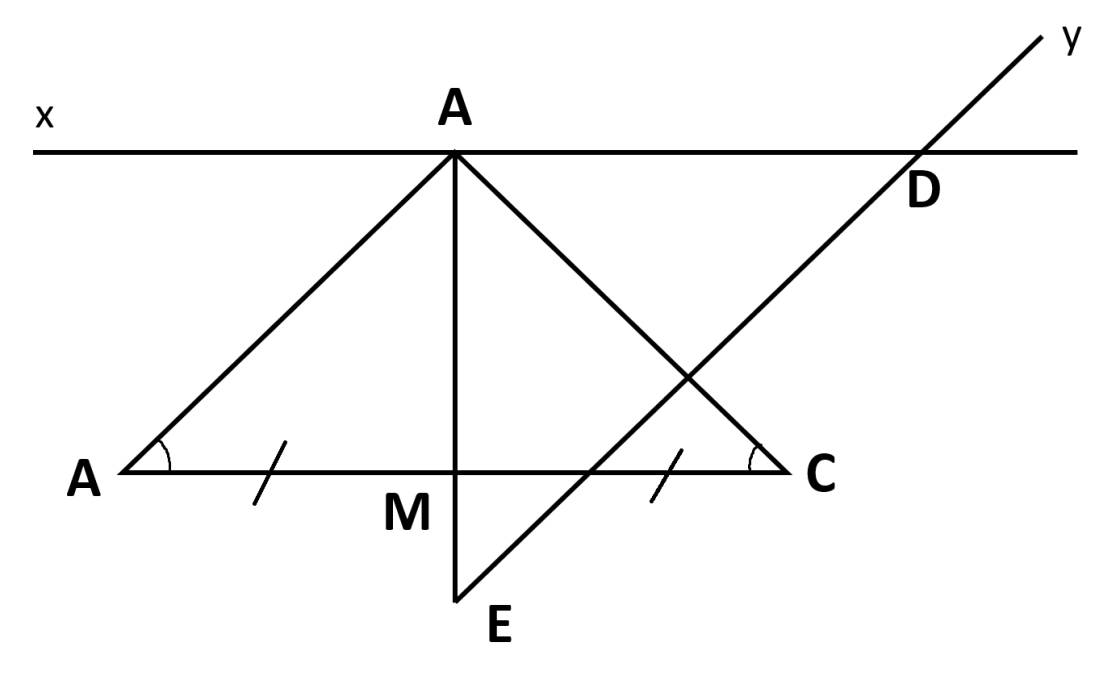
Cho tam giác ABC cân tại A,và điểm M là trung điểm của cạnh BC.Vẽ tia Ax//BC;Cy//AB sao cho Ax cắt Cy tại D.Kéo dài AM cắt tia đối của tia Cy tại điểm E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì ΔABC cân tại A (gt)
⇒ AB = AC (t/c)
Xét ΔABH và ΔACH có:
AH chung
∠HAB = ∠HAC (AH là phân giác của góc A)
AB = AC (cmt)
⇒ ΔABH = ΔACH (c.g.c)
Vậy ΔABH = ΔACH (c.g.c)
b) Vì ΔABH = ΔACH (cmt)
⇒ ∠AHB = ∠AHC (2 góc tương úng)
Ta có: ∠AHB + ∠AHC = 1800 (2 góc kề bù)
⇒ ∠AHB = ∠AHC = 1800/2 = 900
Ta có: ∠AHC + ∠dCH = 1800 (2 góc bù nhau)
T/s: 900 + ∠DCH = 1800
∠DCH = 1800 - 900
∠DCH = 900
⇒ DC⊥CH (đn 2 đt vuông góc)
Vậy DC⊥CH

a ) Xét ∆BAD và ∆CAD
AB = AC ( ∆ABC cân )
\(\widehat{B}=\widehat{C}\)
\(\widehat{BAD}=\widehat{DAC}\)
=> ∆ABH = ∆ACH(g.c.g)

a) Xét \(\Delta MDB=\Delta NEC\left(c-g-c\right)\)
=> DM=NE
b) Ta có
\(\Delta MDI\perp D\)=> DMI+MID=90 độ
\(\Delta NEI\perp E\)=> góc ENI+NIE=90 độ
mà MID=NEI đối đỉnh
=> DMI=ENI
\(=>\Delta MDI=\Delta NEI\left(c-g-c\right)\)
=> IM=ỊN
=> BC cắt MN tại I là trung Điểm của MN
c) Gọi H là chân đường zuông góc kẻ từ A xuống BC
=> tam giác AHB = tam giác AHC( ch, cạnh góc zuông )
=> góc HAB= góc HAC
Gọi O là giao điểm của AH zới đường thẳng zuông góc zới MN kẻ từ I
=> tam giác OAB= tam giác OAC (c-g-c)(1)
=> góc OBA = góc OCA ; OC=OB
tam giác OBM= tam giác OCN (c-g-c)
=> góc OBM=góc OCN (2)
từ 1 zà 2 suy ra OCA=OCN =90 độ do OC zuông góc zới AC
=> O luôn cố đinhkj
=> DPCM

anh/chị tự kẻ hình nhé :v
a, t\g BAC vuông cân tại A (gt)
=> AC = CB (đn) và AC _|_ AB (đn) mà AD đối AC
=> AB _|_ AD
xét tam giác ACB và tam giác ADB có : AB chung
AC = AD (gt)
AB _|_ AC và AD => góc CAB = góc DAB = 90
=> tam giác ACB = tam giác ADB (2cgv)
=> BC = DB (đn)
=> tam giác BDC cân tại B (đn)
b, M là trung điểm của BC (gt) => CM = 1/2BC
N là trung điểm của BD (gt) => DN = 1/2DB
mà BC = DB (cmt)
=> CM = DN
xét tam giác CDM và tam giác DCN có : CD chung
góc MCA = góc ADN do tam giác ACB = tam giác ADB (câu a)
=> tam giác CDM và tam giác DCN (c - g - c)
=> CN = DM (đn)

Bài 3
a) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E có
AB=AC( vì tam giác ABC cân tại A)
Góc A chung
=> Tam giác ABD= tam giác ACE ( cạnh huyền- góc nhọn)
b) Có tam giác ABD= tam giác ACE( theo câu a)
=> AE=AD ( 2 cạnh tương ứng)
=> Tam giác AED cân tại A
c) Xét các tam giác vuông AEH và ADH có
Cạnh huyền AH chung
AE=AD
=> Tam giác AEH=tam giác ADH ( cạnh huyền- cạnh góc vuông)
=>HE=HD
Ta có AE=AD và HE=HD hay AH là đường trung trực của ED
d) Ta có AB=AC, AE=AD
=>AB-AE=AC-AD
=>EB=DC
Xét tam giác EBC vuông tại E và tam giác DCK vuông tại D có
BD=DK
EB=Dc
=> tam giác EBC= tam giác DCK ( 2 cạnh góc vuông)
=> Góc ECB= góc DEC ( 2 góc tương ứng)
Bài 1:
Xét tam giác ABM và tam giác ACM có:
AB=AC(tam giác ABC cân tại A)
BM=MC(gt)
AM cạnh chung
Suy ra tam giác ABM= tam giác ACM (c-c-c)
b) Xét hai tam giác vuông MBH và MCK có:
BM=MC(gt)
góc ABC=góc ACB (tam giác ABC cân tại A)
Suy ra tam giác MBH= tam giác MCK (ch-gn)
Suy ra BH=CK
c) MK vuông góc AC (gt)
BP vuông góc AC (gt)
Suy ra MK sông song BD
Suy ra góc B1= góc M2 (đồng vị)
Mà M1=M2(Tam giác HBM= tam giác KCM)
Suy ra góc B1= góc M1
Suy ra tam giác IBM cân
xong bài 1 đẻ bài 2 mình nghĩ tiếp