(z-3)^2-(x-2y)^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

21 tháng 1 2022
b: \(=\dfrac{12\left(y-z\right)^4+3\left(y-z\right)^5}{6\left(y-z\right)^2}=2\left(y-z\right)^2+\dfrac{1}{2}\left(y-z\right)^3\)

BH
1 tháng 3 2020
\(\hept{\begin{cases}x^2-2x\sqrt{y}+2y=x\\y^2-2y\sqrt{z}+2z=y\\z^2-2z\sqrt{x}+2x=z\end{cases}}\)
\(\Leftrightarrow x^2-2x\sqrt{y}+2y+y^2-2y\sqrt{z}+2z+z^2-2z\sqrt{x}+2x=x+y+z\)
\(\Leftrightarrow\left(x-\sqrt{y}\right)^2+\left(y-\sqrt{z}\right)^2+\left(z-\sqrt{x}\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x-\sqrt{y}=0\\y-\sqrt{z}=0\\z-\sqrt{x}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\sqrt{y}\\y=\sqrt{z}\\z=\sqrt{x}\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}x=y=z=0\\x=y=z=1\end{cases}}\)
TL
0

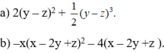
\((z-3)^2-(x-2y)^2\\=[(z-3)-(x-2y)][(z-3)+(x-2y)]\\=(z-3-x+2y)(z-3+x-2y)\)
\(\left(z-3\right)^2-\left(x-2y\right)^2\)
\(=\left[\left(z-3\right)-\left(x-2y\right)\right]\left[\left(z-3\right)+\left(x-2y\right)\right]\)
\(=\left(z-3-x+2y\right)\left(z-3+x-2y\right)\)