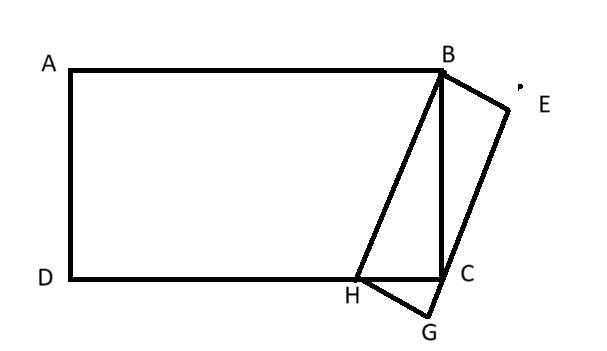
Đề bài: Cho hình trên, biết HC = 1/4 DC và diện tích hình ABEGHD là 180cm2. Hãy tính diện tích hai hình chữ nhật ABCD và BEGH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích hình chữ nhật \(ABCD\) là: \(24\times11=264\left(cm^2\right)\)
b) Diện tích hình tam giác \(ADM\) là: \(\dfrac{1}{2}\times11\times16=88\left(cm^2\right)\)
c) Diện tích hình tam giác \(ABC\) là: \(\dfrac{1}{2}\times24\times11=132\left(cm^2\right)\)
Diện tích hình tam giác \(AMC\) là: \(264-88-132=44\left(cm^2\right)\)

Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có: BC = BM = MN = 3 cm Chiều cao tương ứng cạnh DC của hình bình hành ABCD là: 8 : 4 = 2 (cm) Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là : 3 x 2 = 6 (cm2 ) Đáp số: 6 cm2

Vì DM = 1/3 DC nên DT tam giác ACD = 3 lần DT tam giác ADM
Mà DT hình chữ nhật ABCD gấp 2 lần DT tam giác ACD
Nên DT hình chữ nhật ABCD là :
15 x 3 x 2 = 90 cm2
Hạ \(CK\perp BH\) tại K
\(S_{BCH}=\dfrac{1}{2}xBHxCK\)
\(S_{BEGH}=BHxGH=BHxCK\)
\(\Rightarrow S_{BCE}+S_{CHG}=S_{BEGH}-S_{BCH}=\dfrac{1}{2}xBHxCK=S_{BCH}\)
Ta có
\(HC=\dfrac{1}{4}DC\Rightarrow DC=4xHC\)
\(S_{BCH}=\dfrac{1}{2}xBCxHC\)
\(S_{ABCD}=BCxDC=BCx4xHC\)
\(\Rightarrow\dfrac{S_{BHC}}{S_{ABCD}}=\dfrac{1}{8}\Rightarrow S_{ABCD}=8xS_{BCH}\)
Ta có
\(S_{ABEGHD}=S_{ABCD}+S_{BCE}+S_{CHG}=8xS_{BCH}+S_{BCH}=9xS_{BCH}=180cm^2\)
\(\Rightarrow S_{BCH}=180:9=20cm^2\)
\(\Rightarrow S_{ABCD}=8xS_{BCH}=8x20=160cm^2\)
\(S_{BEGH}=S_{BCH}+S_{BCE}+S_{CHG}=2xS_{BCH}=2x20=40cm^2\)