Cho x, y không âm thỏa mãn x2 + y2 = 2
Tìm GTNN của P = x + 3y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2\leq (x+y)[(29x+3y)+(29y+3x)]=32(x+y)^2\leq 32.(x^2+y^2)(1+1)=64(x^2+y^2)\leq 64.2=128$
$\Rightarrow P\leq 8\sqrt{2}$
Vậy $P_{\max}=8\sqrt{2}$

Áp dụng bất đẳng thức Cosi ta có:
1 32 32 x 29 x + 3 y ≤ 1 4 2 32 x + 29 x + 3 y 2 = 1 8 2 61 x + 3 y
Tương tự
1 32 32 y 29 y + 3 x ≤ 1 8 2 61 y + 3 x
=> P ≤ 4 2 x + y ≤ 4 2 x 2 + 1 2 + y 2 + 1 2 = 8 2
Vậy P min = 8 2 <=> x = y = 1

mk copy trên trang này
https://lazi.vn/edu/exercise/311935/cho-cac-so-thoa-man-2x-3y-13-tim-gia-tri-nho-nhat-cua-q
\(2x+3y=13\Rightarrow y=\dfrac{13-2x}{3}\)
\(Q=x^2+\left(\dfrac{13-2x}{3}\right)^2=\dfrac{13}{9}x^2-\dfrac{52}{9}x+\dfrac{169}{9}\)
\(Q=\dfrac{13}{9}\left(x-2\right)^2+13\ge13\)
\(Q_{min}=13\) khi \(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)

Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B

Chọn C.
Phương pháp:
Đưa biểu thức P về hàm số 1 ẩn x.
Khảo sát, tìm GTNN của hàm số đó.
Cách giải:
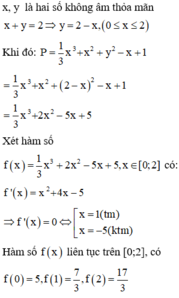
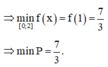

Đáp án A
P = 1 3 x 3 + x 2 + y 2 − x + 1 = = 1 3 x 3 + x + y 2 − 2 x y − x + 1 = 1 3 x 3 + 4 − 2 x 2 − x − x + 1
⇒ P = 1 3 x 3 + 2 x 2 − 5 x + 5
xét hàm số P x trên 0 ; 2 ta có
P ' = x 2 + 4 x − 5 ⇒ P ' = 0 ⇔ x = 1
Ta tính các giá trị P 0 = 5 ; P 1 = 7 3 ; P 2 = 17 3 ⇒ M i n P = 7 3
Ta có:
\(x^2+y^2=2\)
\(\Rightarrow0\le x\le\sqrt{2}\)
\(0\le y\le\sqrt{2}\)(1)
Lại có:
\(P=x+3y\)
\(\Rightarrow3y\ge0\) (1)
Để P nhỏ nhất thì x hoặc 3y đạt giá trị nhỏ nhất vì x và 3y đều lớn hơn 0.
Xét trường hợp x nhỏ nhất:
\(x\ge0\) dấu bằng xảy ra \(\Leftrightarrow x=0\Rightarrow y=\sqrt{2}\)
\(\Rightarrow P=3\sqrt{2}\)
Xét trường hợp y nhỏ nhất.
\(y\ge0\) dấu bằng xảy ra \(\Leftrightarrow y=0\Rightarrow x=\sqrt{2}\)
\(\Rightarrow P=\sqrt{2}\)
Vậy giá trị nhỏ nhất của P tại \(\left(x,y\right)=\left(\sqrt{2},0\right)\)