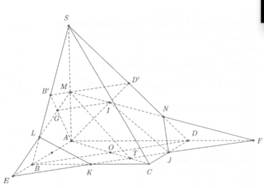
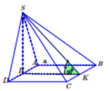
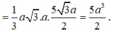Chóp S.ABCD có I,J,K nằm trong tam giác SAB, SBC, SAD. Tìm thiết diện của mặt phẳng (IJK) và chóp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2018
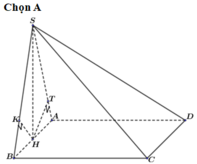
Đáp án A
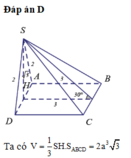
Gọi H là trung điểm của AB .
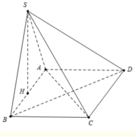
Lại có: S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Do A D / / B C nên giao tuyến d của (SAD) và (SBC) đi qua S và song song với AD.
Do A D ⊥ A B A D ⊥ S H ⇒ A D ⊥ S A B ⇒ d ⊥ S A B .Suy ra góc giữa hai mặt phẳng (SAD) và (SBC) bằng 180 ∘ − AS B ⏜ = 60 ∘ .
25 tháng 12 2023
Rất rõ ràng là câu A nhé bạn, vì \(O\in AC\subset\left(SAC\right)\)
AM
27 tháng 12 2021
a. \(\left(SAB\right)\cap\left(SBC\right)=?\)
Ta có: \(\left\{{}\begin{matrix}S\in\left(SAB\right),\left(SBC\right)\\B\in\left(SAB\right),\left(SBC\right)\end{matrix}\right.\)\(\Rightarrow\)\(\left(SAB\right)\cap\left(SBC\right)=SB\)
b. \(\left(SAB\right)\cap\left(SCD\right)=?\)
Xét mp (SAB), kẻ Sx//AB
Ta có: Sx//AB, AB//CD \(\Rightarrow\) CD//Sx
Lại có: \(S\in\left(SAB\right),\left(SCD\right)\)
\(\Rightarrow\)\(\left(SAB\right)\cap\left(SCD\right)=Sx\)
c. \(\left(SAD\right)\cap\left(SBC\right)=?\)
Xét mp (ABCD), ta có không song song với BC
Gọi \(I=AD\cap BC\)
Ta có: \(\left\{{}\begin{matrix}S\in\left(SAD\right),\left(SBC\right)\\I\in\left(SAD\right),\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\)\(\left(SAD\right)\cap\left(SBC\right)=SI\)
