giá trị của biểu thức
2018x2019-19/2019x2017+2000 giúp mik với ạHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=11\cdot\dfrac{16}{55}\cdot\dfrac{15}{8}=\dfrac{11\cdot5}{55}\cdot\dfrac{16}{8}\cdot3=2\cdot3=6\)

a: \(A=\dfrac{-1}{3}\cdot\dfrac{-2}{3}\cdot\dfrac{3}{2}\cdot x^2y\cdot xy^3\cdot xy^2=\dfrac{1}{3}x^4y^6\)
Hệ số là 1/3
Bậc là 10
b: \(P=\dfrac{1}{25}+3\cdot\dfrac{1}{5}\cdot\left(-1\right)+1=\dfrac{26}{25}-\dfrac{3}{5}=\dfrac{26}{25}-\dfrac{15}{25}=\dfrac{11}{25}\)
a)A= -\(\dfrac{1}{3}\)x2y. -\(\dfrac{2}{3}\)xy3. 1\(\dfrac{1}{2}\)xy2
A=(-\(\dfrac{1}{3}\).-\(\dfrac{2}{3}\).1\(\dfrac{1}{2}\)). (x2.x.x). (y.y3.y2)
A=1.x4.y6
_Hệ số là:1
_Bậc của đơn thức A là 10

\(M=\frac{2022x-2020}{3x+2}=\frac{2022x+1348-3368}{3x+2}\)
\(=674-\frac{336}{3x+2}\)
Bạn lập bảng là xog.
TL:
\(M=\frac{2022x-2020}{3x-2}=\frac{2022x+1348-3368}{3x-2}\)
\(=674-\frac{336}{3x+2}\)
_HT_

Với $x=1$ ta có :
$-7.(x+3)^3 .|2x-1|+42$
$=-7.(-1+3)^3.|2.(-1)-1|+42$
$=-7.2^3.|-3|+42$
$=-7.8.3 + 42$
$=-126$

a: Số cần tìm là 5,32:0,125=42,56
b: \(A=1+\dfrac{1}{2019}-1-\dfrac{1}{2018}+\dfrac{1}{2018}-\dfrac{1}{2019}=0\)

\(P=\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
Ta có: \(xyz=1\Rightarrow x=\dfrac{1}{yz}\)
\(P=\left(\dfrac{1}{yz}+yz\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(yz+\dfrac{1}{yz}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+2+1y^2z^2+y^2+2+\dfrac{1}{y^2}+z^2+2+\dfrac{1}{z^2}-\left(y^2z+z+\dfrac{1}{z}+\dfrac{1}{y^2z}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+y^2z^2+y^2+\dfrac{1}{y^2}+z^2+\dfrac{1}{z^2}+6-y^2z^2-y^2-z^2-1-1-\dfrac{1}{z^2}-\dfrac{1}{y^2}-\dfrac{1}{y^2z^2}\)\(P=\left(\dfrac{1}{y^2z^2}-\dfrac{1}{y^2z^2}\right)+\left(y^2z^2-y^2z^2\right)+\left(y^2-y^2\right)+\left(z^2-z^2\right)+\left(\dfrac{1}{y^2}-\dfrac{1}{y^2}\right)+\left(\dfrac{1}{z^2}-\dfrac{1}{z^2}\right)+4\)
\(P=4\)
Vậy: ...
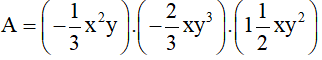
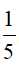 ; y = -1
; y = -1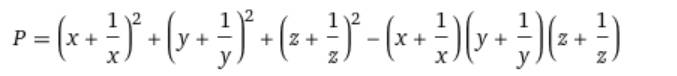
\(\dfrac{2018x2019-19}{2019x2017+2000}=\dfrac{\left(2017+1\right)x2019-19}{2019x2017+2000}\\ =\dfrac{2017x2019+1x2019-19}{2017x2019+2000}=\dfrac{2017x2019+2000}{2017x2019+2000}=1\)