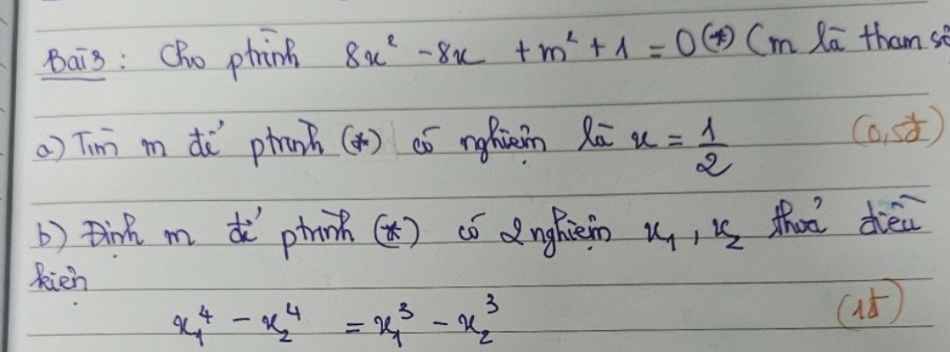 giúp e câu b với ạ
giúp e câu b với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 2023 ko phải là năm nhuận
b: Sin nhật thứ 15 là vào ngày 8/4/2024
Vì 2024là năm nhuận nên sinh nhật lần 15 là vào thứ hai

a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)

b) \(B=\left(x^3-3x^2y+3xy^2-y^3\right)-6\left(x^2-2xy+y^2\right)+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-6\left(x-y\right)^2+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-3\cdot2\cdot\left(x-y\right)^2+3\cdot2^2\cdot\left(x-y\right)-2^3\)
\(B=\left[\left(x-y\right)-2\right]^3\)
\(B=\left(x-y-2\right)^3\)
f) \(F=\left(8x^3+12x^2y+6xy^2+y^3\right)+3\left(4x^2+4xy+y^2\right)y+3\left(2x+y\right)y^2+y^3\)
\(F=\left(2x+y\right)^3+3\left(2x+y\right)^2y+3\left(2x+y\right)y^2+y^3\)
\(F=\left[\left(2x+y\right)+y\right]^3\)
\(F=\left(2x+y+y\right)^3\)
\(F=\left(2x+2y\right)^3\)
b: =(x-y)^3-6(x-y)^2+12(x-y)-2^3
=(x-y-2)^3
f: =(2x+y)^3+3(2x+y)^2*y+3*(2x+y)*y^2+y^3
=(2x+y+y)^3
=(2x+2y)^3

Bạn chỉ cần áp dụng cái phân tích đa thức thành nhân tử bằng phương pháo đặt nhân tử chung là ra rồi

b: Xét tứ giác ACOD có
I là trung điểm của CD
I là trung điểm của OA
Do đó: ACOD là hình bình hành
mà OC=OD
nên ACOD là hình thoi
Xét ΔCMO có
CA là đường trung tuyến
CA=MO/2
Do đó: ΔCMO vuông tại C
hay CM là tiếp tuyến của (O)


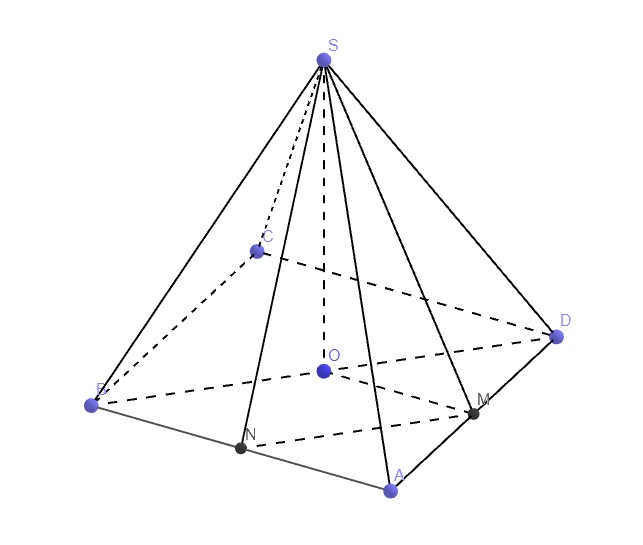
b.
\(SO\perp\left(ABCD\right)\Rightarrow OM\) là hình chiếu vuông gốc của SM lên (ABCD)
\(\Rightarrow\widehat{SMO}\) là góc giữa SM và (ABCD)
\(BD=a\sqrt{2}\Rightarrow SO=\sqrt{SD^2-OD^2}=\sqrt{3a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{10}}{2}\)
\(OM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow tan\widehat{SMO}=\sqrt{10}\Rightarrow\widehat{SMO}=...\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(SM;BD\right)}=\widehat{\left(SM;MN\right)}=\widehat{SMN}\)
\(OM=ON\Rightarrow SN=SM=\sqrt{SO^2+OM^2}=\dfrac{a\sqrt{11}}{2}\)
Định lý hàm cos:
\(cos\widehat{SMN}=\dfrac{SM^2+MN^2-SN^2}{2SM.MN}=\dfrac{\sqrt{22}}{22}\Rightarrow\widehat{SMN}=...\)

Câu 2
\((1) MnO_2 + 4HCl \to MnCl_2 + Cl_2 + 2H_2O\\ (2) Cl_2 + H_2 \xrightarrow{as} 2HCl\\ (3) 3Cl_2 + 2Fe \xrightarrow{t^o} 2FeCl_3\\ (4) 2FeCl_3 + Fe \to 3FeCl_2\\ (5) 2NaOH + Cl_2 \to NaCl + NaClO + H_2O\)
\((1) 4Al + 3O_2 \xrightarrow{t^o} 2Al_2O_3\\ (2) 2Fe + 3Cl_2 \xrightarrow{t^o} 2FeCl_3\\ (3) C + O_2 \xrightarrow{t^o} CO_2\\ (4) 2KMnO_4 \xrightarrow{t^o} K_2MnO_4 + MnO_2 + O_2\\ (5) 4P + 5O_2 \xrightarrow{t^o} 2P_2O_5\\ (6) 2KClO_3 \xrightarrow{t^o} 2KCl + 3O_2\\ (7) Fe + H_2SO_4 \to FeSO_4 + H_2\\ (8) Cu + 2H_2SO_4 \to CuSO_4 + SO_2 + 2H_2O\\ (9) 2Fe + 6H_2SO_4 \to Fe_2(SO_4)_3 + 3SO_2 + 6H_2O\\ (10) 2Al + 6H_2SO_4 \to Al_2(SO_4)_3 + 3SO_2 + 6H_2O\)



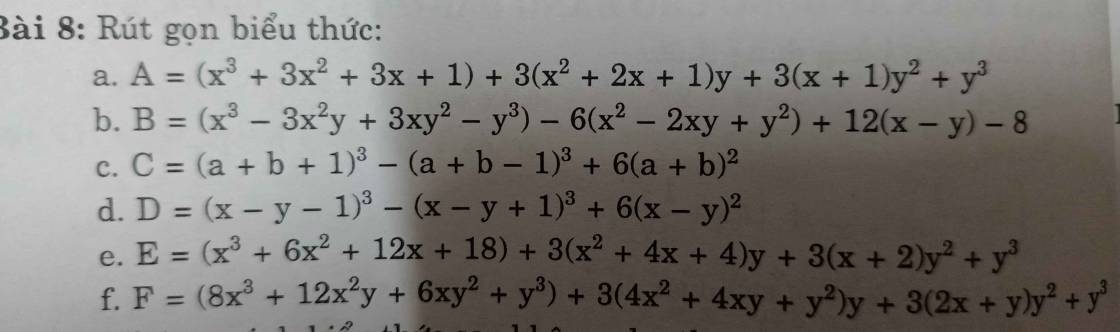



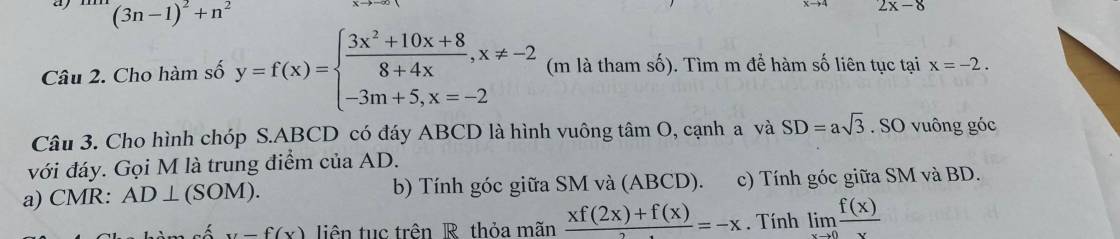

Lời giải:
$\Delta' (*) = 4^2-8(m^2+1)=8-8m^2$
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'(*) = 8-8m^2\geq 0\Leftrightarrow 1-m^2\geq 0$
$\Leftrightarrow -1\leq m\leq 1$
Áp dụng định lý Viet:
$x_1+x_2=1$
$x_1x_2=\frac{m^2+1}{8}$
Khi đó:
$x_1^4-x_2^4=x_1^3-x_2^3$
$\Leftrightarrow (x_1^2-x_2^2)(x_1^2+x_2^2)=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)$
$\Leftrightarrow (x_1-x_2)[(x_1+x_2)(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)[1(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)(-x_1x_2)=0$
$\Leftrightarrow (x_1-x_2).\frac{-(m^2+1)}{8}=0$
$\Leftrightarrow x_1-x_2=0$ (do $m^2+1\geq 1>0$ với mọi $m$ nên số này khác 0)
$\Leftrightarrow x_1=x_2$
Kết hợp $x_1+x_2=1$
$\Rightarrow x_1=x_2=\frac{1}{2}$
$\frac{m^2+1}{8}=x_1x_2=\frac{1}{4}$
$\Leftrightarrow m^2+1=2$
$\Leftrightarrow m^2=1\Leftrightarrow m=\pm 1$ (tm)