Cho hình vuông ABCD. Trên AB lấy điểm M sao cho AM = MB, nối M với D, M với C.
a) Hỏi diện tích hình tam giác DMC gấp mấy lần diện tích hình tam giác DMA?
b) AC cắt MD tại N. Biết diện tích tam giác AND là 5 cm2. Tính diện tích hình vuông ABCD.
Giúp mình với ạ

Lời giải:
a.
$\frac{S_{DMC}}{S_{DMA}}=\frac{AD\times DC}{2}: \frac{AM\times AD}{2}=\frac{AD\times DC}{AM\times AD}=\frac{DC}{AM}=\frac{AB}{\frac{AB}{2}}=2$
Vậy diện tích tam giác DMC gấp 2 lần diện tích tam giác DMA
b.
Kẻ đường cao AH của tam giác $ADM$ và đường cao $CK$ của tam giác $DCM$
Ta có:
$2=\frac{S_{DCM}}{S_{DMA}}=\frac{CK\times MD}{2}: \frac{AH\times DM}{2}=\frac{CK}{AH}$
Suy ra:
$\frac{S_{ADN}}{S_{DNC}}=\frac{AH\times DN}{2}: \frac{CK\times DN}{2}=\frac{AH}{CK}=\frac{1}{2}$
$2\times S_{ADN}=\times S_{DNC}$
$3\times S_{ADN}=S_{DNC}+S_{ADN}=S_{ADC}=AD\times DC:2=S_{ABCD}:2$
$S_{ABCD}=3\times S_{ADN}\times 2=6\times S_{ADN}=6\times 5=30$ (cm2)
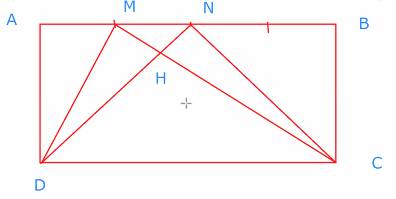
Hình vẽ: