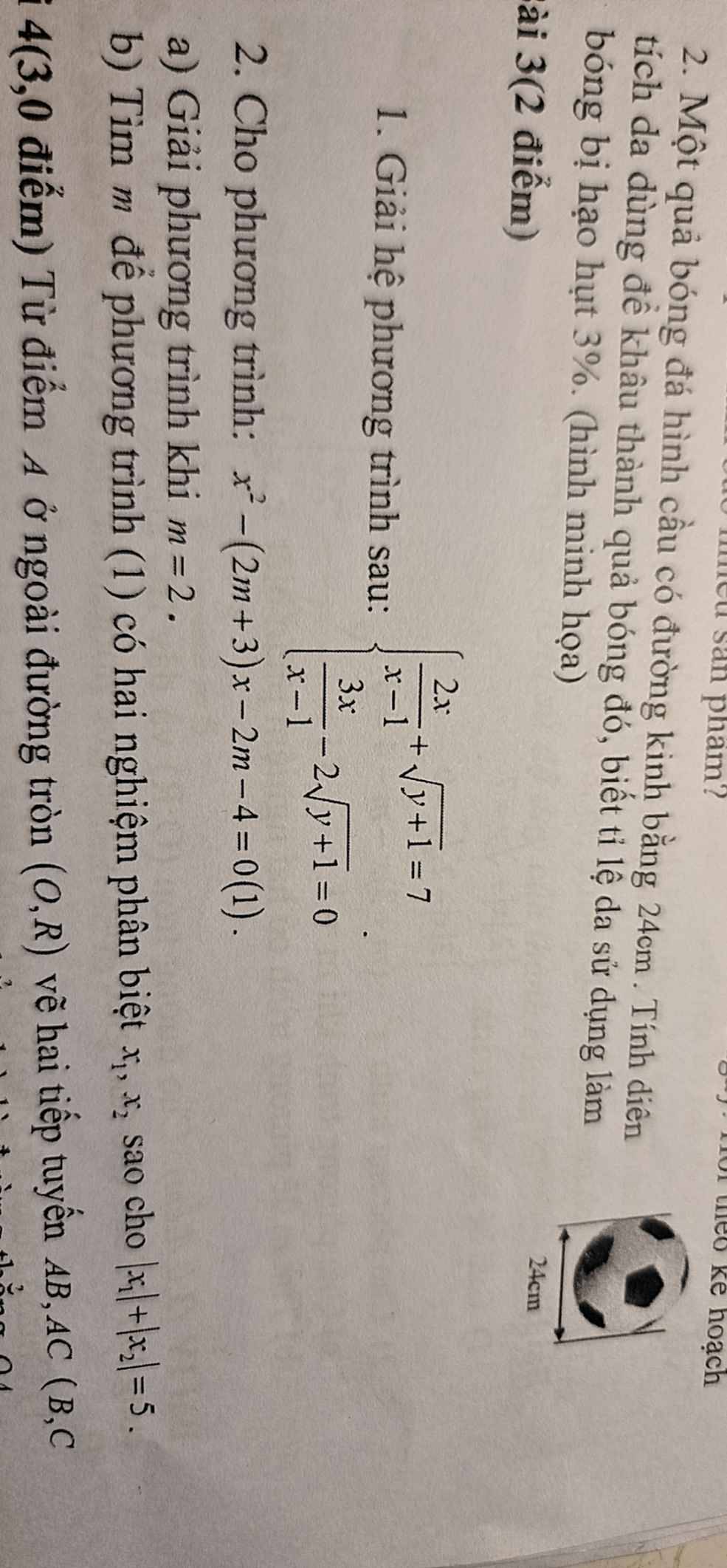 giúp e bài 3 ý 2b với ạ
giúp e bài 3 ý 2b với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`@` `\text {Ans}`
`\downarrow`
`2,`
`a)`
\(\left(5^4+4^7\right)\cdot\left(8^9-2^7\right)\cdot\left(2^4-4^2\right)\)
`= (5^4 + 4^7) . (8^9 - 2^7) . (2^4 - (2^2)^2)`
`= (5^4 + 4^7) . (8^9 - 2^7) . (2^4 - 2^4)`
`= (5^4 + 4^7) . (8^9 - 2^7) . 0`
`= 0`
`b)`
\(\left(7^{2003}+7^{2002}\right)\div7^{2001}\)
`=`\(7^{2003}\div7^{2001}+7^{2002}\div7^{2001}\)
`=`\(7^{2003-2001}+7^{2002-2001}\)
`=`\(7^2+7=49+7=56\)

Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)


Câu 1:
a: x/1.25=3.5/2.5=7/5
=>x=1.75
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{2.1}{7}=0.3\)
Do đó: x=1,2; y=0,9


\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)

2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)

a) \(3\left(x-y\right)^2+9y\left(y-x\right)^2\)
\(=3\left(x-y\right)^2+9y\left(x-y\right)^2\)
\(=\left(x-y\right)^2\left(3-9y\right)\)
\(=3\left(x-y\right)^2\left(3y+1\right)\)
b) \(3\left(x-y\right)^2+9y\left(y-x\right)\)
\(=3\left(y-x\right)^2+9y\left(y-x\right)\)
\(=\left(y-x\right)\left[3\left(y-x\right)+9y\right]\)
\(=3\left(y-x\right)\left(y-x+3y\right)\)
\(=3\left(y-x\right)\left(4y-x\right)\)
a: =3(x-y)^2+9y(x-y)^2
=(x-y)^2(3+9y)
=(x-y)^2*3*(y+3)
b: =3(x-y)^2-9y(x-y)
=3(x-y)(x-y-9y)
=3(x-y)(x-10y)

d: \(\Leftrightarrow x^2-x-1=x+2\)
\(\Leftrightarrow x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
e: \(\Leftrightarrow x^2-x-2+x-1=3x+4\)
\(\Leftrightarrow x^2-3-3x-4=0\)
\(\Leftrightarrow x^2-3x-7=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-7\right)=37\)
Vì Δ>0 nên pt có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{37}}{2}\\x_2=\dfrac{3+\sqrt{37}}{2}\end{matrix}\right.\)

\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16\)
\(=\left(m-4\right)^2>0\) khi \(m\ne4\)
Câu 3.2
Để pt có 2 nghiệm pb thì:
$\Delta=(2m+3)^2+4(2m+4)>0$
$\Leftrightarrow (2m+3)^2+4(2m+3)+4>0$
$\Leftrightarrow (2m+3+2)^2>0\Leftrightarrow (2m+5)^2>0$
$\Leftrightarrow 2m+5\neq 0$
$\Leftrightarrow m\neq \frac{-5}{2}$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt (1) thì:
$x_1+x_2=2m+3$
$x_1x_2=-2m-4$
$\Rightarrow x_1+x_2+x_1x_2+1=0$
$\Leftrightarrow (x_1+1)(x_2+1)=0$
$\Leftrightarrow x_1=-1$ hoặc $x_2=-1$
Nếu $x_1=-1$ thì $x_2=2m+4$. Nếu $x_2=-1$ thì $x_1=2m+4$
Không mất tổng quát giả sử $x_1=-1; x_2=2m+4$
Khi đó:
$|x_1|+|x_2|=5$
$\Leftrightarrow |-1|+|2m+4|=5$
$\Leftrightarrow |2m+4|=4$
$\Leftrightarrow 2m+4=\pm 4$
$\Leftrightarrow m=0$ hoặc $m=-4$
Do $m> \frac{-5}{2}$ nên $m=0$