Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ đánh số từ 1 đến 8, 7 viên bi màu xanh đánh số từ 1 đến 7, và 5 viên bi màu vàng đánh số từ 1 đến 5. Lấy ngẫu nhiên ra 5 viên bi, tính xác suất để 5 viên bi lấy ra có đủ 3 mầu và có tổng số chấm trên 3 bi là 1 số chia hết cho 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số .
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4=16 cách (do số bi đỏ ít hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh).
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4=12cách.
● Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3=9 cách.
Suy ra số phần tử của biến cố A là 16+12+9=37.
Vậy xác suất cần tính 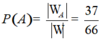 .
.
Chọn B.

Không gian mẫu: \(C_{27}^3\)
Chọn 1 quả cầu xanh: có 8 cách
Chọn quả cầu đỏ khác số so với quả xanh: 8 cách
Chọn quả vàng khác số so với 2 quả đã chọn trước đó: 8 cách
\(\Rightarrow8.8.8\) cách chọn thỏa mãn
Xác suất: \(P=\dfrac{8.8.8}{C_{27}^3}=...\)

Gọi A là biến cố lấy ra được 3 viên bi màu đỏ.
Số cách lấy 3 viên bi từ 20 viên bi là C 20 3 nên ta có Ω = C 20 3 = 1140 .
Số cách lấy 3 viên bi màu đỏ là C 8 3 = 56 nên Ω A = 56 .
Do đó: P ( A ) = 56 1140 = 14 285
Đáp án B

Đáp án A
+ Sắp xếp các viên bi thành ba hàng lần lượt là hàng 1 gồm 4 viên vi vàng đánh số từ 1 đến 4; hàng 2 gồm các 5 viên bi đỏ đánh số từ 1 đến 5, hàng 3 gồm 6 viên bi xanh đánh số từ 1 đến 6 (đóng thẳng cột như hình vẽ).
+ Việc lựa chọn tiến hành theo ba bước sau:
Bước 1: Chọn 1 viên bi vàng ở hàng thứ nhất: có 4 cách thực hiện.
Sau đó ta xóa đi cột chứa viên bi vàng vừa được chọn.
Bước 2: Chọn 1 viên bi đỏ từ hàng thứ hai từ 4 viên bi đỏ còn lại (1 viên bi đỏ bị loại bỏ sau bước thứ nhất): có 4 cách thực hiện.
Sau đó ta tiếp tục xóa cột chứa viên bi đỏ vừa được chọn.
Bước 3: Chọn 1 viên bi xanh từ 4 viên bi xanh còn lại ở hàng thứ ba: có 4 cách chọn.
Vậy theo quy tắc nhân, có: 4.4.4 = 64 cách chọn thỏa mãn.


Đáp án A
Sắp xếp các viên bi thành ba hàng lần lượt là hàng 1 gồm 4 viên vi vàng đánh số từ 1 đến 4; hàng 2 gồm các 5 viên bi đỏ đánh số từ 1 đến 5, hàng 3 gồm 6 viên bi xanh đánh số từ 1 đến 6 (đóng thẳng cột như hình vẽ).

Việc lựa chọn tiến hành theo ba bước sau:
Bước 1: Chọn 1 viên bi vàng ở hàng thứ nhất: có 4 cách thực hiện.
Sau đó ta xóa đi cột chứa viên bi vàng vừa được chọn.
Bước 2: Chọn 1 viên bi đỏ từ hàng thứ hai từ 4 viên bi đỏ còn lại (1 viên bi đỏ bị loại bỏ sau bước thứ nhất): có 4 cách thực hiện.
Sau đó ta tiếp tục xóa cột chứa viên bi đỏ vừa được chọn.
Bước 3: Chọn 1 viên bi xanh từ 4 viên bi xanh còn lại ở hàng thứ ba: có 4 cách chọn.
Vậy theo quy tắc nhân, có: ![]() cách chọn thỏa mãn
cách chọn thỏa mãn

Có \(C_{24}^3\) cách chọn 3 viên bất kì.
Có \(C_8^3+C_6^3+C_{10}^3\) cách họn 3 viên bi cùng màu.
Có 6 cách chọn 3 viên bi cùng số.
\(\Rightarrow\) Có \(C_{24}^3-\left(C_8^3+C_6^3+C_{10}^3\right)-6=1822\) cách chọn 3 viên bi khác màu, khác số.
Chọn 1 viên xanh: có 6 cách
Chọn 1 viên đỏ khác số viên xanh: 7 cách
Chọn 1 viên vàng khác số viên xanh và đỏ: 8 cách
Tổng cộng: \(6.7.8=336\) cách

Ba bi khác màu nên phải chọn từ mỗi hộp 1 viên bi.
Chọn từ hộp thứ ba 1 viên: có 4 cách chọn.
Chọn từ hộp thứ hai 1 viên có số khác với viên bi đã chọn từ hộp ba: có 4 cách chọn
Chọn từ hộp thứ nhất 1 viên bi có số khác với số của hai viên đã chọn từ hộp một và hai: có 4 cách chọn.
Vậy Ω A = 4 3 = 64 .
Đáp án B

Gọi A là biến cố: “trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
Trong hộp có tất cả: 5+ 15 + 35 = 55 viên bi
- Số phần tử của không gian mẫu: Ω = C 55 7 .
- A ¯ là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào.”
=> n A ¯ = C 20 7 .
Vì A và A ¯ là hai biến cố đối nên: n A = Ω − n A ¯ = C 55 7 − C 20 7 .
Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là P A = C 55 7 − C 20 7 C 55 7 .
Chọn đáp án B.

a. Mỗi viên bi đánh một số, nên 2 viên bi lấy ra mang số khác nhau. Vậy
Ω={(m,n)|1≤n≤7 và m≠n}
Chọn B
