giúp mình câu 5b với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


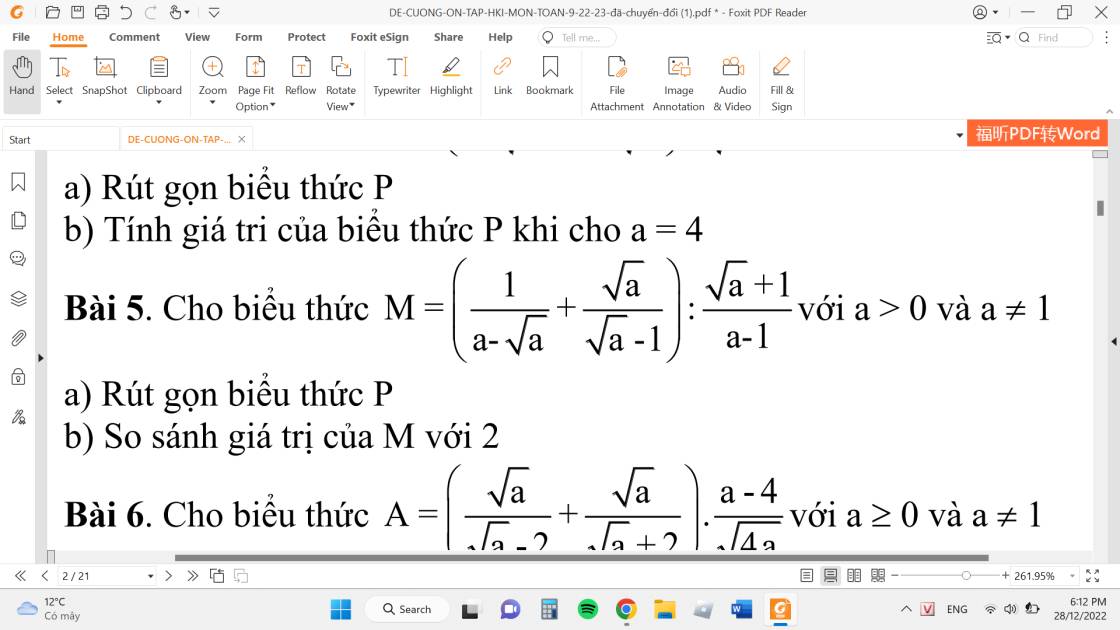
Bài 5:
a: \(M=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{a-1}{\sqrt{a}+1}=\dfrac{a+1}{\sqrt{a}}\)
b: \(M-2=\dfrac{a+1-2\sqrt{a}}{\sqrt{a}}=\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}}>0\)
=>M>2



Câu 11.
a)Độ tự cảm của ống dây:
\(L=4\pi\cdot10^{-7}\cdot\dfrac{N^2}{l}S=4\pi\cdot10^{-7}\cdot\dfrac{1000^2}{0,2}\cdot50\cdot10^{-4}=0,0314H=0,0314\cdot10^3=31,4mH\)
b)Độ biến thiên từ thông:
\(\Delta\Phi=L\cdot\Delta i=0,0314\cdot\left(1-0\right)=0,0314Wb\)
Suất điện động cảm ứng:
\(e_{tc}=\left|-\dfrac{\Delta\Phi}{\Delta t}\right|=\left|-\dfrac{0,0314}{0,1}\right|=0,314V\)

A) \(x-\dfrac{2}{3}=\dfrac{4}{5}\\ x=\dfrac{4}{5}+\dfrac{2}{3}\)
\(x=\dfrac{22}{15}\)
b)\(\dfrac{7}{9}-x=\dfrac{1}{3}\\ x=\dfrac{7}{9}-\dfrac{1}{3}\\ x=\dfrac{4}{9}\)
C)\(x:\dfrac{2}{3}=\dfrac{9}{8}\\ x=\dfrac{9}{8}x\dfrac{2}{3}\\ x=\dfrac{3}{4}\)

a)
Ta có : (6x+11y) chia hết cho 31
=> 6x+11y+31y chia hết cho 31 ( Vì 31 chia hết cho 31)
=> 6x+42y chia hết cho 31
=>6.(x+7y) chia hết cho 31
=> x+7y chia hết cho 31
b)
3a+5b=8c⇔3(a−c)=5(c−b)(∗)⇒3(a−c)⋮53a+5b=8c⇔3(a−c)=5(c−b)(∗)⇒3(a−c)⋮5, mà (3,5)=1(3,5)=1 nên a−c⋮5a−c⋮5
Vì −8≤a−c≤9−8≤a−c≤9 nên a−c∈−5;0;5a−c∈−5;0;5
Với a−c=−5(1)a−c=−5(1), Thế vào (*), được: b−c=3(2)b−c=3(2). Từ (1), (2) suy ra: a−b=−8a−b=−8 hay b=a+8⇒a=1,b=9,c=6b=a+8⇒a=1,b=9,c=6. Ta được số 196.
Với a−c=0a−c=0 hay a=ca=c loại vì 3 chữ số khác nhau.
Với a−c=5a−c=5 lập luận tương tự, ta được:
b=0;a=8;c=3b=0;a=8;c=3. Ta được số 803.
b=1;a=9;c=4b=1;a=9;c=4. Ta được số 914.
Vậy có tất cả 3 số thỏa mãn đề bài.


K = a² - 2ab + 5b² - 4b + 9
= (a² - 2ab + b²) + (4b² - 4b + 1) + 8
= (a - b)² + (2b - 1)² + 8
Do (a - b)² ≥ 0 với mọi a, b ∈ R
(2b - 1)² ≥ 0 với mọi b R
⇒ (a - b)² + (2b - 1)² ≥ 0 với mọi a, b ∈ R
⇒ (a - b)² + (2b - 1)² + 8 ≥ 8 với mọi a, b ∈ R
Vậy GTNN của K là 8 khi a = b = 1/2

Ta có: \(\dfrac{a}{b}=\dfrac{3}{5}\)
\(\Leftrightarrow\dfrac{a}{3}=\dfrac{b}{5}\)
Đặt \(\dfrac{a}{3}=\dfrac{b}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3k\\b=5k\end{matrix}\right.\)
Ta có: \(\dfrac{2a-4b}{a-5b}\)
\(=\dfrac{2\cdot3k-4\cdot5k}{3k-5\cdot5k}=\dfrac{6k-20k}{3k-25k}\)
\(=\dfrac{-14k}{-22k}=\dfrac{7}{11}\)

Answer:
Câu 1: đề khó hiểu quá nên mình bỏ qua nhé!
Câu 2:
Có:
\(2a=3b\)
\(\Rightarrow\frac{2a}{6}=\frac{3b}{6}\)
\(\Rightarrow\frac{a}{3}=\frac{b}{2}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}\)
\(5b=7c\)
\(\Rightarrow\frac{5b}{35}=\frac{7c}{35}\)
\(\Rightarrow\frac{b}{7}=\frac{c}{5}\)
\(\Rightarrow\frac{b}{14}=\frac{c}{10}\)
\(\Leftrightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{a}{21}=\frac{b}{14}=\frac{c}{10}=\frac{3a+5c-7b}{3.21+5.10-7.14}=\frac{30}{15}=2\)
\(\Rightarrow\hept{\begin{cases}a=42\\b=28\\c=20\end{cases}}\)



Câu 5:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
ΔBAD=ΔBED
=>\(\widehat{BDA}=\widehat{BDE}\)
mà \(\widehat{BDA}=\widehat{DBK}\)(BK//AC)
nên \(\widehat{KBD}=\widehat{KDB}\)
=>ΔKBD cân tại K