Cho tam giác ABC vuông góc với A tại điểm B mỗi góc bằng 60⁰ . Tính diện tích hình thang đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9 2016
AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm
2 tháng 2 2022
Bài 1:
a: \(AB=21\cdot\dfrac{3}{7}=9\left(cm\right)\)
AC=21-9=12(cm)
=>BC=15(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=7,2(cm)
Xét ΔAHB vuông tại H có \(AB^2=AH^2+BH^2\)
hay BH=5,4(cm)
=>CH=9,6(cm)
1 tháng 4 2016
H�nh tam gi�c TenDaGiac1: Polygon B, A, C H�nh tam gi�c TenDaGiac1_1: Polygon B', A', C' G�c ?: G�c gi?a G, B, B' G�c ?: G�c gi?a G, B, B' G�c ?: G�c gi?a B, A, C G�c ?: G�c gi?a B, A, C ?o?n th?ng c: ?o?n th?ng [B, A] c?a H�nh tam gi�c TenDaGiac1 ?o?n th?ng a: ?o?n th?ng [A, C] c?a H�nh tam gi�c TenDaGiac1 ?o?n th?ng b: ?o?n th?ng [C, B] c?a H�nh tam gi�c TenDaGiac1 ?o?n th?ng c_1: ?o?n th?ng [B', A'] c?a H�nh tam gi�c TenDaGiac1_1 ?o?n th?ng a_1: ?o?n th?ng [A', C'] c?a H�nh tam gi�c TenDaGiac1_1 ?o?n th?ng b_1: ?o?n th?ng [C', B'] c?a H�nh tam gi�c TenDaGiac1_1 ?o?n th?ng d: ?o?n th?ng [B', B] ?o?n th?ng e: ?o?n th?ng [C', C] ?o?n th?ng f: ?o?n th?ng [A', A] ?o?n th?ng g: ?o?n th?ng [B', G] ?o?n th?ng h: ?o?n th?ng [B, G] ?o?n th?ng i: ?o?n th?ng [G, M] B = (-2.08, 1.4) B = (-2.08, 1.4) B = (-2.08, 1.4) A = (3.04, 1.4) A = (3.04, 1.4) A = (3.04, 1.4) C = (0.1, -0.66) C = (0.1, -0.66) C = (0.1, -0.66) B' = (0.38, 4.84) B' = (0.38, 4.84) B' = (0.38, 4.84) A' = (5.5, 4.84) A' = (5.5, 4.84) A' = (5.5, 4.84) C' = (2.56, 2.78) C' = (2.56, 2.78) C' = (2.56, 2.78) ?i?m G: (B + A + C) / 3 ?i?m G: (B + A + C) / 3 ?i?m G: (B + A + C) / 3 ?i?m M: Trung ?i?m c?a C, A ?i?m M: Trung ?i?m c?a C, A ?i?m M: Trung ?i?m c?a C, A
Góc giữa BB' và (ABC) là \(\widehat{B'BG}=60^0\). Suy ra đường cao \(B'G=BB'.\sin60^0=\dfrac{a\sqrt{3}}{2}\)
Lại có \(BG=BB'.\cos60^0=\dfrac{a}{2}\)
Gọi M là trung điểm AC thì \(BM=\dfrac{3}{2}BG=\dfrac{3a}{4}\)
Đặt AC=x thì \(BC=AC.\tan 60^0=x\sqrt{3}\)
Suy ra \(BM=\sqrt{BC^2+CM^2}=\sqrt{3x^2+\dfrac{x^2}{4}}=\dfrac{x\sqrt{13}}{2}=\dfrac{3a}{4}\). Suy ra \(x=\dfrac{3a\sqrt{13}}{26}\)
Do đó \(S_{ABC}=\dfrac{1}{2}BC.AC=\dfrac{x^2\sqrt{3}}{2}=\dfrac{9a^2\sqrt{3}}{52}\)
Vậy \(V_{A'ABC}=\dfrac{1}{3}BB'.S_{ABC}=\dfrac{3a^2\sqrt{3}}{52}\)
1 tháng 4 2016
Gọi G là trong tâm tam giác ABC ta có B′G⊥(ABC)Từ đó B′BCG^=600 là góc mà B′B′ tạo với mặt phẳng (ABC). Trong tam giác vuông BB′G ta có ngay: BG=a2,B′G=a3√2BG=a2,B′G=a32
Đặt AB=2xAB=2x, trong tam giác vuông ABCABC ta có:
AC=x,BC=x3√AC=x,BC=x3 (do ABCˆ=600ABC^=600)
Giả sử BG∩ACBG∩AC thì BN=a2BG=3a4BN=a2BG=3a4.
Áp dụng định lí py ta go trong tam giác vuông BNCBNC ta có:
BN2=NC2+BC2⇒9a216=x24+3x2⇒x2=9a252(1)BN2=NC2+BC2⇒9a216=x24+3x2⇒x2=9a252(1)
ta có VA′ABC=13SABC.B′G=13.12.AB.BC.a3√2=a3√12x.x3√=ax24(2)VA′ABC=13SABC.B′G=13.12.AB.BC.a32=a312x.x3=ax24(2)
thay (2)(2) vào (1)(1) ta có: VA′.ABC=9a3208VA′.ABC=9a3208 (đvtt)
CM
22 tháng 9 2018
Đáp án D.
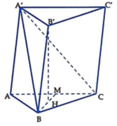
Gọi H là trọng tâm của tam giác ABC, từ giả thiết suy ra B ' H ⊥ A B C .
Khi đó
B B ' , A B C ^ = B B ' , B H ^ = B ' B H ^ = 60 °
Ta có
B B ' = a ⇒ B H = B B ' . cos B ' B H ^ = a . cos 60 ° = a 2 , B ' H = B ' B 2 − B H 2 = a 3 2
Gọi M là trung điểm BC, suy ra B H = 2 3 B M ⇒ B M = 3 2 B H = 3 2 . a 2 = 3 a 4 .
Đặt A C = x > 0 ⇒ B C = A C . tan B A C ^ = x . tan 60 ° = x 3 ⇒ A B = A B 2 + A C 2 = 2 x .
Lại có
B M = B C 2 + C M 2 = B C 2 + A C 2 4 = 3 x 2 + x 2 4 = x 13 2 = 3 a 4 ⇒ x = 3 a 2 13
⇒ A C = 3 a 2 13 , B C = 3 3 a 2 13 , A B = 6 a 2 13 ⇒ S Δ A B C = 1 2 A C . B C = 9 3 a 2 104
(đvdt).
Vậy V A ' A B C = 1 3 B ' H . S Δ A B C = 1 3 . a 3 2 . 9 3 a 2 104 = 9 a 3 208 (đvtt).
CM
27 tháng 6 2019
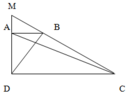
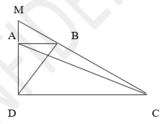
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )
Em ghi đề cho chính xác lại