cho biết A = 1400
B =700
C =1500
chứng minh rằng Ax // Cy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


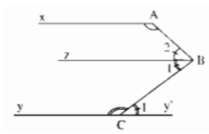
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ∠A +∠(B2 ) =180o
(2 góc trong cùng phía) (1)
Theo giả thiết ta có: ∠A +∠B + ∠C =360o (gt)
Hay ∠A +∠(B2 ) +∠(BCy) =360o (2)
Từ (1)và (2)suy ra :
∠(B1) + ∠BCy = 180o (3)
Lại có: ∠(C1 ) + ∠BCy =180o (hai góc kề bù) (4)
Từ (3) và (4) suy ra: ∠(B1 ) =∠(C1 )
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra : Ax // Cy

Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy.
Ta có: ∠(B2 ) +∠(xAB) =180o
(hai góc trong cùng phía)
Mà ∠(xAB) =140o(gt)
Suy ra: ∠(B2 ) =180-∠(xAB) =180o-140o=40o
Mà: ∠(B1 ) +∠(B2 ) =∠(ABC)
Suy ra ∠(B1 ) =∠(ABC) -(B2 ) =70o-40o=30o (1)
∠(yCB) +∠(BCy') =180o(2 góc kề bù)
∠BCy'=180o-∠(yCB) =180o-150o=30o (2)
Từ (1) và (2) ta có: ∠(B1 ) =∠(BCy')
Suy ra: Cy’ // Bz ( vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra Ax // Cy

Qua B kẻ tia Bz//Ax(Bz và Ax nằm khác phía so với đường thẳng AB)
Ta có: Bz//Ax
=>\(\widehat{zBA}=\widehat{xAB}\)
Ta có: \(\widehat{zBA}+\widehat{zBC}=\widehat{ABC}\)
\(\widehat{xAB}+\widehat{yCB}=\widehat{ABC}\)
mà \(\widehat{zBA}=\widehat{xAB}\)
nên \(\widehat{zBC}=\widehat{yCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bz//Cy
mà Ax//Bz
nên Ax//Cy

\(\left\{{}\begin{matrix}ax+by=c\\bx+cy=a\\cx+ay=b\end{matrix}\right.\)
Cộng đại số => \(ax+by+bx+cy+cx+ay=a+b+c\)
<=>\(\left(a+b+c\right)x+\left(a+b+c\right)y=a+b+c\)
<=>\(\left(a+b+c\right)\left(x+y\right)=a+b+c\)
<=>\(\left(a+b+c\right)\left(x+y\right)-\left(a+b+c\right)=0\)
<=>\(\left(a+b+c\right)\left(x+y-1\right)=0\)
+TH1:\(\left(a+b+c\right)=0\)
=>\(a+b=-c\)
=>\(\left(a+b\right)^3=-c^3\)
=>\(a^3+b^3+3a^2b+3ab^2=-c^3\)
=>\(a^3+b^3+3ab\left(a+b\right)=-c^3\)
=>\(a^3+b^3+c^3=-3ab\left(a+b\right)\)
Mà a+b=-c => -3ab(a+b)=-3ab(-c)=3abc
=>\(a^3+b^3+c^3=3abc\)
+TH2:x+y=1
<=>y=1-x
=>\(\left\{{}\begin{matrix}ax+b\left(1-x\right)=c\\bx+c\left(1-x\right)=a\\cx+a\left(1-x\right)=b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}ax+b-bx=c\\bx+c-cx=a\\cx+a-ax=b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(a-b\right)x=c-b\\\left(b-c\right)x=a-c\\\left(c-a\right)x=b-a\end{matrix}\right.\)
Nếu \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\)
=>a=b=c
\(\Rightarrow a^3+b^3+c^3=3a^3\\ 3abc=3a^3\\ \Rightarrow a^3+b^3+c^3=3abc\)
Nếu \(\left\{{}\begin{matrix}a-b\ne0\\b-c\ne0\\c-a\ne0\end{matrix}\right.\)=>\(\left\{{}\begin{matrix}x=\dfrac{c-b}{a-b}\left(1\right)\\x=\dfrac{a-c}{b-c}\left(2\right)\\x=\dfrac{b-a}{c-a}\end{matrix}\right.\)
Ta có : (1)=(2)=x suy ra \(\dfrac{c-b}{a-b}=\dfrac{a-c}{b-c}\Rightarrow\dfrac{b-c}{b-a}=\dfrac{a-c}{b-c}\Rightarrow\left(b-c\right)\left(b-c\right)=\left(a-c\right)\left(b-a\right)^{ }\Rightarrow b^2-2bc+c^2=a^2+ab-bc+ca\)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ca=0\)
\(\Rightarrow2\left(a^2+b^2+c^2-ab-bc-ca\right)=0\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ac+a^2=0\\ \\ \\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
=>a=b=c(đưa về trường hợp như trên)

Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:
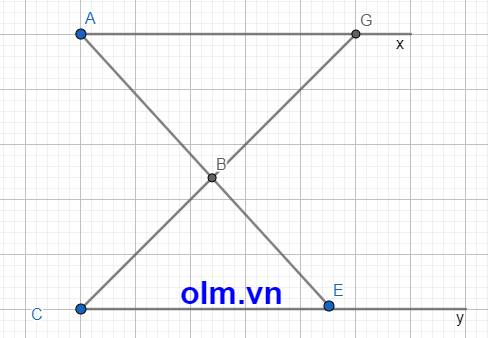
\(\widehat{ABC}\) = \(\widehat{GBE}\) (1) (vì đối đỉnh)
\(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{ABC}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) (3)
Từ (1); (2); (3) ta có: \(\widehat{BCE}\) + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\)
⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)
Mà hai góc CEB và góc GAB là hai góc ở vị trí so le trong nên
Cy // Ax (đpcm)

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp