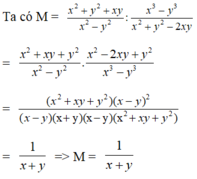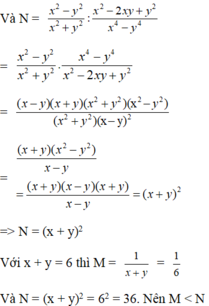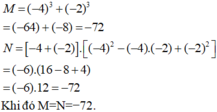So sánh M = 1+ x + x2+...+x2002 và N = x2003 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
9 tháng 6 2018
2 - x 2001 - 1 = 1 - x 2002 - x 2003
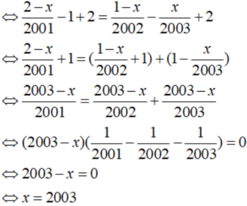
Phương trình có nghiệm x = 2003
PT
22 tháng 4 2021
Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910
KV
29 tháng 4 2022
Ta có:
\(-2018m>-2018n\)
\(\Rightarrow-2018m.\left(-\dfrac{1}{2018}\right)< -2018n.\left(-\dfrac{1}{2018}\right)\)
\(\Rightarrow m>n\)
b) \(x^2-x\left(x+2\right)>3x-1\)
\(\Leftrightarrow x^2-x^2-2x>3x-1\)
\(\Leftrightarrow-2x-3x>-1\)
\(\Leftrightarrow-5x>-1\)
\(\Leftrightarrow x< \dfrac{1}{5}\)
Vậy S = {\(x\) | \(x< \dfrac{1}{5}\)}
29 tháng 4 2022
a) Ta có: -2018m > -2018n
\(\Leftrightarrow-2018m\times\left(\dfrac{-1}{2018}\right)< -2018n\times\left(\dfrac{-1}{2018}\right)\)
\(\Leftrightarrow\) m < n
NT
0
4 tháng 3 2022
Bài 2:
a: a>=b
=>5a>=5b
=>5a+10>=5b+10
b: a>=b
=>-8a<=-8b
=>-8a-9<=-8b-9<-8b+3