giải dùm em câu 37 với ạ , em cảm ơn nhiều nha.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
4 tháng 9 2021
Câu 34:
|vmax| = A.ω = 31,4 (cm/s) \(\Rightarrow\) A = \(\dfrac{\left|v_{max}\right|}{\omega}\)
Ta có công thức: vmin = \(\dfrac{S_{min}}{\Delta t}\)(*)
vì Δt < \(\dfrac{T}{2}\) (\(\dfrac{T}{6}\) < \(\dfrac{T}{2}\))
\(\Rightarrow\)Smin = 2.A. (1 - cos \(\dfrac{\Delta\phi}{2}\)) (Δϕ là góc ở tâm mà bán kính quét được qua khoảng thời gian Δt ấy, có công thức: Δϕ = ω. Δt)
Mấu chốt của bài này là bạn phải đưa biểu thức (*) về chỉ còn một ẩn là |vmax| thôi nhé! (Sử dụng công thức ω = \(\dfrac{2\pi}{T}\) để rút gọn)
(*) \(\Leftrightarrow\) vmin = \(\dfrac{2.A.\left[1-cos\left(\dfrac{\omega.\Delta t}{2}\right)\right]}{\Delta t}\)
\(\Leftrightarrow\) vmin = \(\dfrac{2.\dfrac{\left|v_{max}\right|}{\omega}.\left[1-cos\left(\omega.\dfrac{T}{6.2}\right)\right]}{\dfrac{T}{6}}\) (ở bước này là mình thay các biểu thức trên kia vào nhé)
\(\Leftrightarrow\) vmin = \(\dfrac{2.\left|v_{max}\right|\left[1-cos\left(\dfrac{2\pi}{T}.\dfrac{T}{12}\right)\right]}{\dfrac{T}{6}.\dfrac{2\pi}{T}}\)
Giờ thì ngồi rút gọn T thôi nào!
\(\Leftrightarrow\) vmin = \(\dfrac{2\left|v_{max}\right|.\left(1-cos\dfrac{\pi}{6}\right)}{\dfrac{\pi}{3}}\)
Thay |vmax| = 31,4 và π = 3,14. *Lưu ý là cos \(\dfrac{\pi}{6}\) = \(\dfrac{\sqrt{3}}{2}\) luôn nha (đừng thay π = 3,14 vào đấy!)
\(\Rightarrow\) vmin = \(\dfrac{6.31,4.\left(1-\dfrac{\sqrt{3}}{2}\right)}{3,14}\) = 8,038475773... (cm/s) \(\approx\) 8,04 (cm/s)
Vậy đáp án cần tìm là A. 8,04 cm/s
Có gì thắc mắc cứ hỏi nha. Chúc bạn học tốt!
TT
4
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
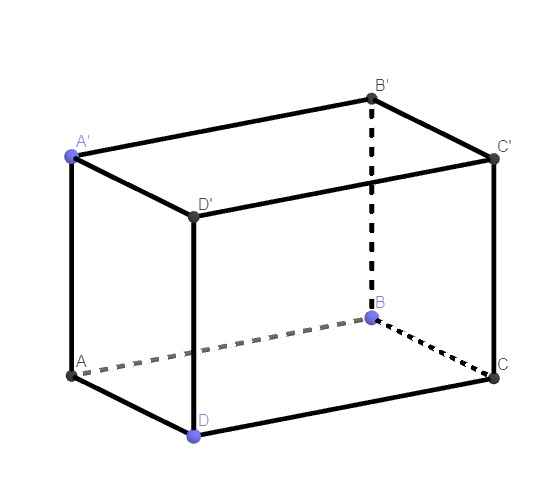
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
VV
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
MT
3
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
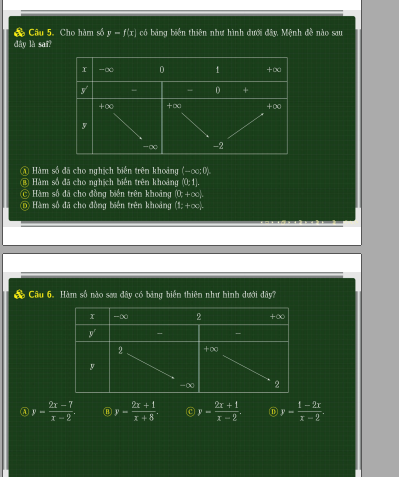
Câu 5:
Nhìn BBT trên \(\left(0;+\infty\right)\) ta thấy trên \(\left(0;1\right)\) đồ thị là đường đi xuống (nghịch biến) nên hàm đồng biến trên toàn miền \(\left(0;+\infty\right)\) là sai
Câu 6:
Từ BBT ta thấy hàm nghịch biến trên các khoảng xác định
\(\Rightarrow\) Loại 2 phương án A và B (ở 2 phương án này hàm đồng biến do y' lần lượt là \(\dfrac{3}{\left(x-2\right)^2}>0\) và \(\dfrac{15}{\left(x+8\right)^2}>0\))
Còn lại 2 phương án C và D, nhìn BBT ta thấy \(y=2\) là tiệm cận ngang (giá trị của y tại x vô cực)
\(\lim\limits_{x\rightarrow\infty}\dfrac{2x+1}{x-2}=2\) (đúng) nên chọn C
7.
Từ BBT ta thấy đây là BBT của hàm bậc 3 \(\Rightarrow\) loại B và D
Từ BBT, y'=0 có 2 nghiệm \(x=0,x=2\)
Ở đáp án A, \(y'=x^2+2x=0\Rightarrow x=0;x=-2\) (ktm)
Nên C đúng (\(y'=x^2-2x=0\Rightarrow x=0;2\))
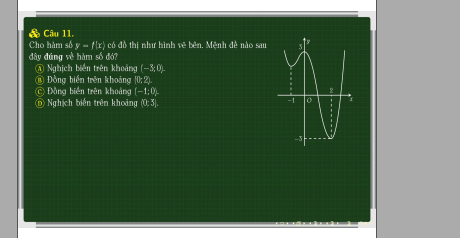
11.
Nhìn đồ thị, ta thấy trên \(\left(-1;0\right)\) đồ thị chỉ có hướng đi lên \(\Rightarrow\) đồng biến trên (-1;0) nên C đúng
(A sai vì trên (-3;0) đồ thị có khoảng đi lên (đồng biến) ở (-1;0)
B sai vì trên (0;2) đồ thị đi xuống => nghịch biến chứ ko phải đồng biến
D sai vì trên (2;3) đồ thị đi lên (đồng biến)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
5C, 6C, 7C, 11C
Cả 4 câu đều C luôn, kì quái thật
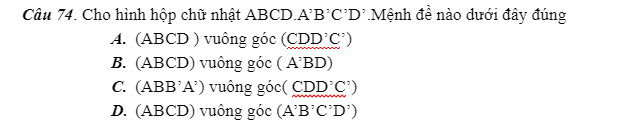
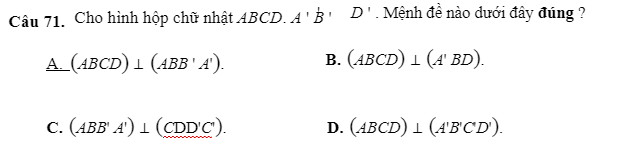
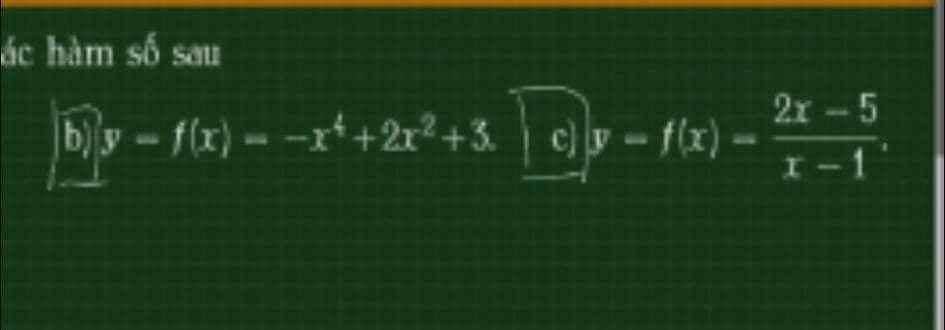
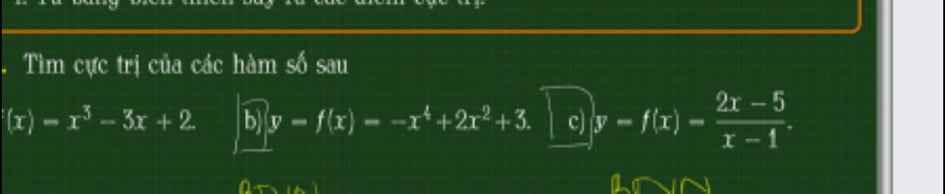
a: ta có: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
=>BD\(\perp\)SC
Câu này còn câu b