Cho tam giác ABC vuông tại A, tia phân giác của
ABC cắt AC tại D. Kẻ DE vuông góc BC (E thuộc BC).
a) Tam giác ABD và tam giác EBD có bằng nhau không ? Vì sao?
b) Kéo dài ED cắt đường thẳng BA tại K. Chứng minh BD vuông góc với KC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
c: Xét ΔAHC vuông tại A và ΔECH vuông tại E có
HC chung
AH=EC
Do đó: ΔAHC=ΔECH
d: Xét ΔBEH vuông tại E và ΔBAC vuông tại A có
BE=BA
BH=BC
Do đó: ΔBEH=ΔBAC
BL
9 tháng 5 2021
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
BL
9 tháng 5 2021
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân
25 tháng 2 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
c: Xét ΔAHC vuông tại A và ΔECH vuông tại E có
CH chung
AH=EC
Do đó: ΔAHC=ΔECH
15 tháng 3 2022
1: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
2: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC
Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
11 tháng 2 2021
A) Xét ΔABD và ΔEBD có:
+) AB=BE (gt)
+) góc ABD= góc EBD (do BD là phân giác góc B)
+) BD chung
=> ΔABD = ΔEBD (c-g-c)
b)
Qua C kẻ đường thẳng vuông góc với BD tại H.
Xét ΔBCF có: BH là đường cao đồng thời là phân giác của góc B
=> ΔBCF cân tại B (tính chất)
=> BC= BF (điều phải chứng minh)
c)
Xét ΔABC và ΔEBF có:
+) AB = EB (gt)
+) góc B chung
+) BC= BF (câu b)
=> ΔABC = ΔEBF (c-g-c)
d)
Từ ý a, ΔABD = ΔEBD (c-g-c)
=> góc BAD= góc BED = 90
=> DE ⊥ BC
Xét ΔBCF có: BH và CA là 2 đường cao cắt nhau tại D
=> D là trực tâm
=> FD ⊥ BC
=> DE trùng với FD
=> D,E,F thẳng hàng
23 tháng 1
Sửa đề: Lấy E thuộc BC sao cho BE=BA
a: Chứng minh ΔBAD=ΔBED
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
=>ΔDEC vuông tại E
c: Sửa đề: Tia BA cắt ED tại F
Ta có: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>AF=EC
11 tháng 4 2020
Câu hỏi của đoàn kiều oanh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
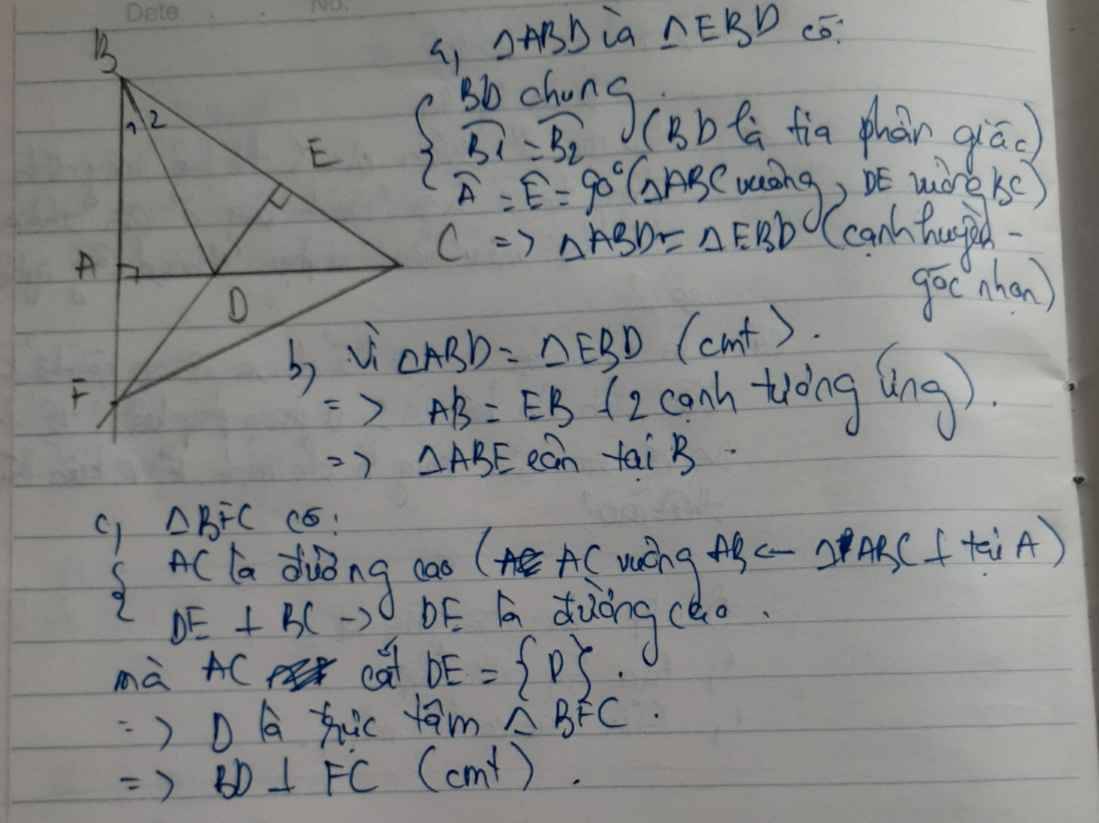
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó ΔBAD=ΔBED
b: Xét ΔBKC có
KE,CA là các đường cao
KE cắt CA tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC