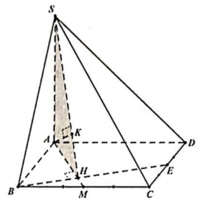
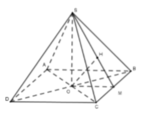
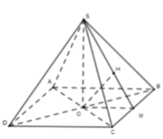
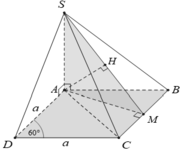
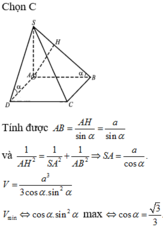
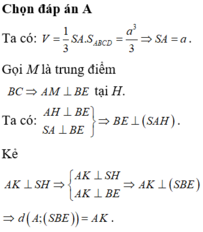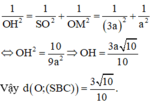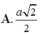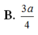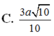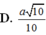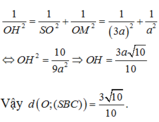Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 6/3 cm và cạnh bên bằng 10 cm.
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách từ 0 đến đường thẳng SA.
c) Tính khoảng cách từ 0 đến mặt bên (SBC).
d) Mặt phẳng trung trực của đoạn thẳng SO cắt các cạnh SA, SB, SC, SD lần lượt tại A, B, C. D' Tính thể tích của khối chóp cụt đều A'B'C'D' ABCD.