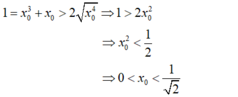Giả sử x0 là nghiệm của phương trình:
x2 + mx + n = 0 và m2 + n2 = 2017
Chứng minh : | x0 | < √2018
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 10 2019
Vì a, b là 2 nghiệm của phương trình x 2 + mx + 1 = 0 nên theo định lí Vi-et ta có:
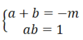
Vì b,c là 2 nghiệm của phương trình x 2 + nx + 2 = 0 nên theo định lí Vi-et ta có:
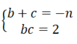
Khi đó:
(b – a)(b – c) = b 2 – bc – ab + ac
= b 2 + bc + ab + ac – 2(ab + bc)
= b( b + c) + a (b + c) – 2 (ab + bc)
= (b + c )( b + a) – 2 (ab + bc)
= (-n).(-m) – 2(1 + 2)
= nm – 6
CH
Cô Hoàng Huyền
Admin
VIP
9 tháng 5 2017
Do x0 là một nghiệm của phương trình nên \(x_0^2+mx_0+n=0\Rightarrow n=-mx_0-x_0^2\)
Thế vào phương trình (2) ta có: \(m^2+\left(-mx_0-x_0^2\right)^2=2017\)
\(\Rightarrow m^2+m^2x_0^2+2mx_0^3+x_0^4-2017=0\)
\(\Rightarrow\left(1+x_0^2\right)m^2+2x_0^3m+\left(x_0^4-2017\right)=0\left(1\right)\)
Để pt (1) có nghiệm thì \(\Delta'\ge0\Rightarrow\left(x_0^3\right)^2-\left(1+x_0^2\right)\left(x_0^4-2017\right)\ge0\)
\(\Rightarrow-x_0^4+2017x_0^2+2017\ge0\)
\(\Rightarrow0\le x_0^2< 2018\Rightarrow\left|x_0\right|< \sqrt{2018}\left(đpcm\right)\)
CM
16 tháng 9 2018
Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
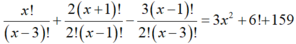
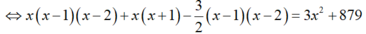
Suy ra x=12.
Chọn B.
CM
30 tháng 10 2019
Gọi x 1 , x 2 là nghiệm của x 2 + p x + q = 0
Gọi x 3 , x 4 là nghiệm của x 2 + m x + n = 0
- Khi đó, theo vi-et: x 1 + x 2 = - p ; x 3 + x 4 = - m , x 3 . x 4 = n
- Theo yêu cầu ta có:
x 1 = x 3 3 x 2 = x 4 3 ⇒ x 1 + x 2 = x 3 3 + x 4 3 ⇔ x 1 + x 2 = ( x 3 + x 4 ) 3 − 3 x 3 x 4 ( x 3 + x 4 )
⇒ p = - m 3 + 3 m n ⇒ p = m 3 - 3 m n
Đáp án cần chọn là: C
CM
29 tháng 11 2017
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].
- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
