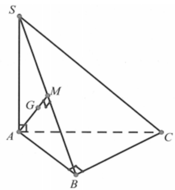
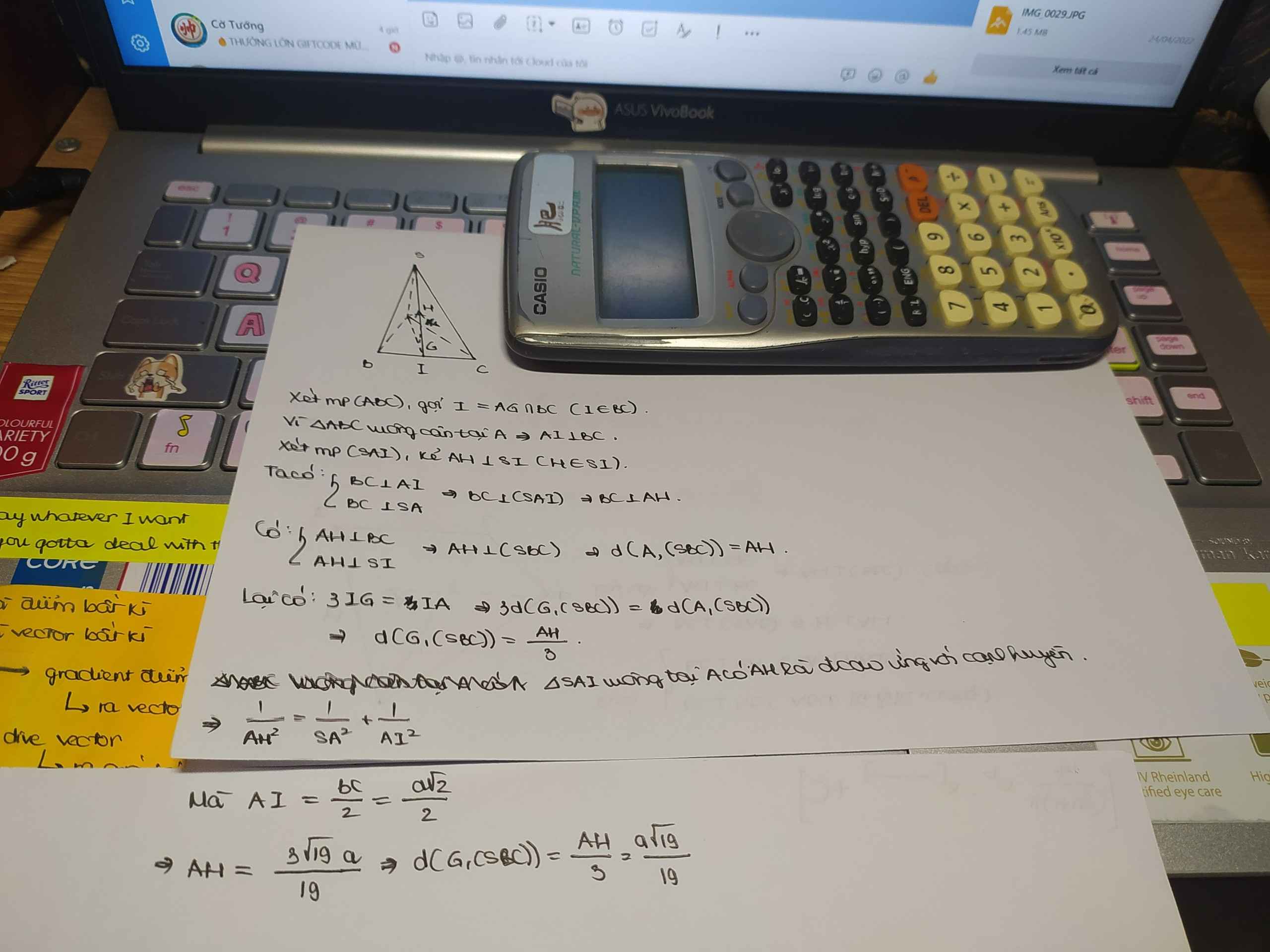
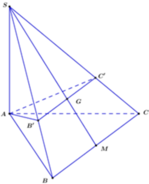
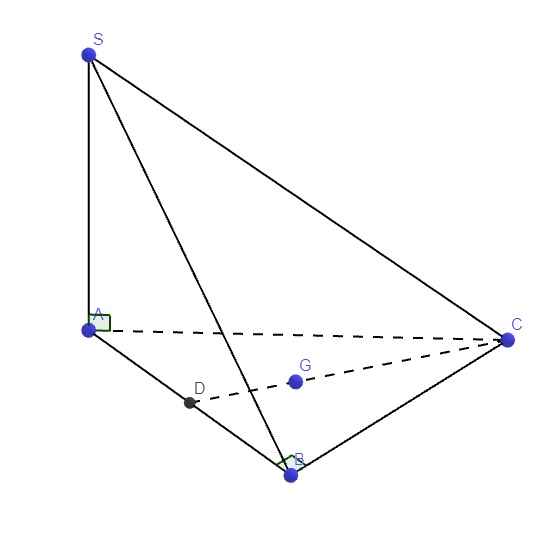
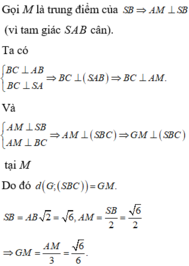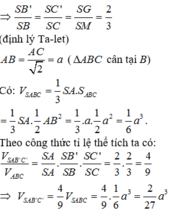Cho hình chóp S.ABC có SA vuông góc với ABC , ABC là tam giác đềucạnh bằng a, SA =2a. Gọi G là trọng tâm. tính d(G,(SBC))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2023
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: Kẻ AK vuông góc SM
=>AK=d(A;(SBC))
AM=4a*căn 3/2=2a*căn 3
=>SM=4a
=>AK=2a*2a*căn 3/4a=a*căn 3
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)
12 tháng 5 2023
a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ